题目内容
15.若函数y=$\frac{3x+27}{x-3}$在区间(a,b)上的值或是(9,+∞),则logab=2.分析 函数y=f(x)=3+$\frac{36}{x-3}$,可知:函数f(x)在(3,+∞)单调递减,由于在区间(a,b)上的值域是(9,+∞),可得a=3,令f(b)=3+$\frac{36}{b-3}$=9,解得b.即可得出.
解答 解:函数y=f(x)=$\frac{3x+27}{x-3}$=$\frac{3(x-3)+36}{x-3}$=3+$\frac{36}{x-3}$,
可知:函数f(x)在(3,+∞)单调递减,
∵在区间(a,b)上的值域是(9,+∞),
∴a=3,
令f(b)=3+$\frac{36}{b-3}$=9,解得b=9.
∴a=3,b=9,
∴logab=log39=2.
故答案为:2.
点评 本题考查了反比例函数的单调性值域、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
20.A为三角形ABC的一个内角.若sinA+cosA=$\frac{12}{25}$,2sinBcosC=sinA,则这个三角形的形状不可能为( )
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 等腰且钝角三角形 | D. | 等腰三角形 |
5.若cosα=$\frac{k+1}{k-3}$,sinα=$\frac{k-1}{k-3}$,则tanα的值为( )
| A. | $\frac{3}{4}$或0 | B. | $\frac{4}{3}$或0 | C. | -$\frac{3}{4}$或0 | D. | -$\frac{4}{3}$或0 |
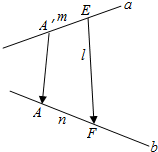 如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.
如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.