题目内容
9.已知函数f(x)对x∈R,都有f(x+2)=f(x),当0≤x≤2时,f(x)=x(2-x),设g(x)=$\left\{\begin{array}{l}{f(x),x≥0}\\{\frac{1}{50}x+1,x<0}\end{array}\right.$,则g(x)的图象中关于y轴对称的点共有( )| A. | 96对 | B. | 100对 | C. | 48对 | D. | 50对 |
分析 根据函数的周期性和对称性求出当x>0,图象关于y轴对称的函数,结合函数的周期性进行求解即可.
解答 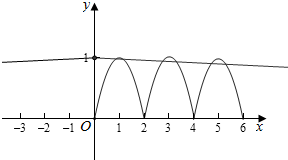 解:由f(x+2)=f(x),得函数的周期为2,
解:由f(x+2)=f(x),得函数的周期为2,
∵当x<0时,g(x)=$\frac{1}{50}x+1$,
∴若x>0时,-x<0,则g(-x)=-$\frac{1}{50}x+1$,
若函数g(x)关于y对称,则g(x)=g(-x)=-$\frac{1}{50}x+1$,
作出对应的图象如图,
当x>0时,由g(x)=-$\frac{1}{50}x+1$=0得x=50,
即有25个周期,每个周期两个函数有2个交点,
则g(x)的图象中关于y轴对称的点共有50对,
故选:D
点评 本题主要考查函数图象的 交点个数的判断,利用偶函数的对称性以及函数的周期性是解决本题的关键.

练习册系列答案
相关题目
14.在△ABC中,若$\frac{a}{cosA}=\frac{b}{cosB}$,则△ABC是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰直角三角形 |
1.若log2(2m+n)=2log2$\sqrt{2mn}$-1,则m+n的取值范围为( )
| A. | [6,+∞) | B. | [3+2$\sqrt{2}$,+∞) | C. | (0,3+2$\sqrt{2}$] | D. | [3+$\sqrt{2}$,6) |