题目内容
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
【答案】(1)![]() ;(2)直线AB过定点Q(0,﹣2).
;(2)直线AB过定点Q(0,﹣2).
【解析】试题分析:(1)根据椭圆的几何性质得到椭圆方程;(2)先由特殊情况得到结果,再考虑一般情况,联立直线和椭圆得到二次函数,根据韦达定理,和向量坐标化的方法,得到结果。
(Ⅰ)由椭圆的离心率e=![]() ,则a2=4b2, 将P(2,1)代入椭圆
,则a2=4b2, 将P(2,1)代入椭圆![]() ,则
,则![]() ,解得:b2=2,则a2=8, ∴椭圆的方程为:
,解得:b2=2,则a2=8, ∴椭圆的方程为: ![]() ;
;
(Ⅱ)当M,N分别是短轴的端点时,显然直线AB为y轴,所以若直线过定点,这个定点一点在y轴上,
当M,N不是短轴的端点时,设直线AB的方程为y=kx+t,设A(x1,y1)、B(x2,y2),
由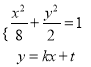 消去y得(1+4k2)x2+8ktx+4t2﹣8=0,·则△=16(8k2﹣t2+2)>0,
消去y得(1+4k2)x2+8ktx+4t2﹣8=0,·则△=16(8k2﹣t2+2)>0,
x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又直线PA的方程为y﹣1=![]() (x﹣2),即y﹣1=
(x﹣2),即y﹣1=![]() (x﹣2),
(x﹣2),
因此M点坐标为(0, ![]() ),同理可知:N(0,
),同理可知:N(0, ![]() ),
),
由![]() ,则
,则![]() +
+![]() =0,
=0,
化简整理得:(2﹣4k)x1x2﹣(2﹣4k+2t)(x1+x2)+8t=0,
则(2﹣4k)×![]() ﹣(2﹣4k+2t)(
﹣(2﹣4k+2t)(![]() )+8t=0,
)+8t=0,
当且仅当t=﹣2时,对任意的k都成立,直线AB过定点Q(0,﹣2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目