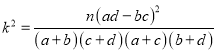题目内容
【题目】设Tn为数列{an}的前n项的积,即Tn=a1a2…an.
(1)若Tn=n2,求数列{an}的通项公式;
(2)若数列{an}满足Tn=![]() (1﹣an)(n∈N*),证明数列
(1﹣an)(n∈N*),证明数列![]() 为等差数列,并求{an}的通项公式;
为等差数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:
①![]() ;
;
②![]() (1≤k≤99,k∈N*).
(1≤k≤99,k∈N*).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问符合条件的数列共有多少个?为什么?
【答案】(1)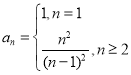 (2)
(2)![]() (3)(Ⅰ)见解析(Ⅱ)299
(3)(Ⅰ)见解析(Ⅱ)299
【解析】
(1)(1)利用作商法求an;
(2)利用等差数列的定义证明数列![]() 为等差数列,并求得{an}的通项公式;
为等差数列,并求得{an}的通项公式;
(3)(Ⅰ)由题意联立方程组求得T4,T5,则由a5=![]() 即得;
即得;
(Ⅱ)由(Ⅰ)可得Tk是方程x2﹣(k+2)x+2=0的一个实根(△>0),当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由Tk+1可得到两个ak+1,即得符合条件的数列共有299个.
(1)当n=1时,a1=T1=1;
当n≥2时,an=![]() ,
,
∴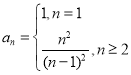
(2)当n=1时,a1=T1=![]() (1﹣a1),所以a1=
(1﹣a1),所以a1=![]() ,
,
当n≥2时,2Tn=1﹣an=1﹣![]() ,
,
所以![]() ﹣
﹣![]() =2,数列{
=2,数列{![]() }为等差数列
}为等差数列
![]() =3+2(n﹣1)=2n+1,Tn=
=3+2(n﹣1)=2n+1,Tn=![]() ,an=1﹣2Tn=
,an=1﹣2Tn=![]()
(3)(Ⅰ)由![]() ,
,![]() ;可得T4=3±
;可得T4=3±![]() ,
,
由![]() ,
,![]() ;可得T5=
;可得T5=![]() ,
,
所以![]() 或
或![]() 或
或![]() 或
或![]()
(Ⅱ)![]() ,
,![]() ,所以a1=1或2
,所以a1=1或2
Tk是方程x2﹣(k+2)x+2=0的一个实根(其中△>0),
当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由Tk+1可得到两个ak+1
所以符合条件的数列共有299个

 习题精选系列答案
习题精选系列答案【题目】某大学为了解学生对学校食堂服务的满意度,随机调查了50名男生和50名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如图所示的列联表.经计算![]() 的观测值
的观测值![]() ,则可以推断出( )
,则可以推断出( )
满意 | 不满意 | |
男 | 30 | 20 |
女 | 40 | 10 |
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
A.该学校男生对食堂服务满意的概率的估计值为![]()
B.调研结果显示,该学校男生比女生对食堂服务更满意
C.有95%的把握认为男、女生对该食堂服务的评价有差异
D.有99%的把握认为男、女生对该食堂服务的评价有差异
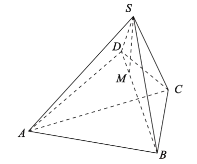
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,O为AC的中点.
,O为AC的中点.
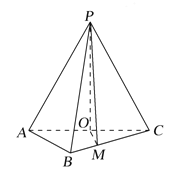
(1)证明:![]() 平面ABC;
平面ABC;
(2)若点M在棱BC上,且![]() ,求点C到平面POM的距离.
,求点C到平面POM的距离.
(3)若点M在棱BC上,且二面角![]() 为30°,求PC与平面PAM所成角的正弦值.
为30°,求PC与平面PAM所成角的正弦值.
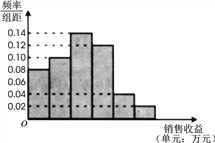
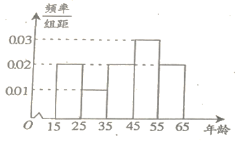
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.