题目内容
8.若曲线f(x)=sinx+$\sqrt{3}$cosx的切线的斜率为k,则k的取值范围是[-2,2].分析 先求出函数的导数,根据导数的几何意义结合两角和的余弦公式,再由余弦函数的图象和性质,即可得到k的范围.
解答 解:∵f(x)=sinx+$\sqrt{3}$cosx,
∴f′(x)=cosx-$\sqrt{3}$sinx
=2($\frac{1}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx)
=2cos(x+$\frac{π}{3}$)∈[-2,2],
则切线的斜率为k∈[-2,2].
故答案为:[-2,2].
点评 理解导数的几何意义和掌握余弦函数的图象和性质是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
3.已知复数z=x+yi(x,y∈R),且|z-2|=$\sqrt{3}$,则$\frac{y+1}{x}$的最大值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 2+$\sqrt{6}$ | D. | 2-$\sqrt{6}$ |
18.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(-3,1),$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则tanθ等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
 已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.
已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.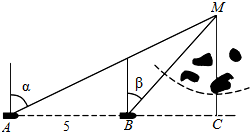 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.