题目内容
已知向量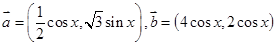 函数
函数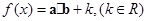
(Ⅰ)求 的单调增区间;
的单调增区间;
(Ⅱ)若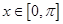 时,
时, 的最大值为4,求
的最大值为4,求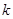 的值.
的值.
(Ⅰ)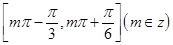 (Ⅱ)
(Ⅱ)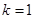
解析试题分析: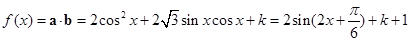
…………3分
(Ⅰ)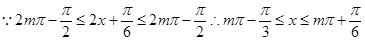
所以 的单调增区间为
的单调增区间为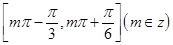 ;
;
(Ⅱ) 在
在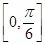 上单调递增,
上单调递增,  在
在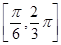 上单调递减,
上单调递减, 在
在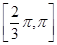 上单调递增,
上单调递增, 所以
所以 的最大值为
的最大值为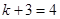 ,所以
,所以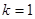
考点:三角函数性质及向量的数量积运算
点评:若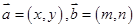 则
则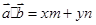 ,求形如
,求形如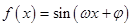 的三角函数单调区间时首先将
的三角函数单调区间时首先将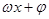 看做一个整体在相应的单调区间内
看做一个整体在相应的单调区间内

练习册系列答案
相关题目
有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响。
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
(1)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径;
(2)若通过公路1、公路2的“一次性费用”分别为3.2万元、1.6万元(其它费用忽略不计),此项费用由生产商承担。如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天销售商将少支付给生产商2万元。如果汽车A、B长期按(1)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大。
(注:毛利润=(销售商支付给生产商的费用)—(一次性费用))
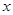 米.
米.
 ,
,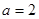 时,解不等式
时,解不等式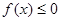 ;
;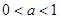 ,解关于
,解关于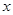 的不等式
的不等式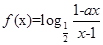 为奇函数,
为奇函数,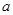 为常数,
为常数, 在区间
在区间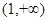 上单调递增;
上单调递增;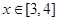 ,不等式
,不等式 恒成立,求实数
恒成立,求实数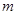 的取值范围。
的取值范围。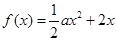 ,
,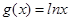 .
.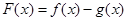 ,求函数
,求函数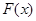 的单调区间;
的单调区间; 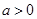 ,使得方程
,使得方程 在区间
在区间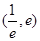 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.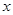 元/千克,政府补贴为
元/千克,政府补贴为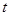 元/千克,根据市场调查,当
元/千克,根据市场调查,当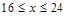 时,这种食品市场日供应量
时,这种食品市场日供应量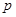 万千克与市场日需量
万千克与市场日需量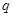 万千克近似地满足关系:
万千克近似地满足关系: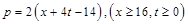 ,
,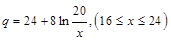 。当
。当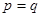 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。