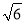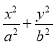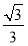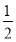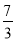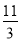题目内容
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
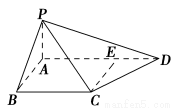
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=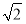 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
(1)见解析(2)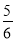
【解析】(1)证明 因为PA⊥平面ABCD,CE?平面ABCD,
所以PA⊥CE.
因为AB⊥AD,CE∥AB,
所以CE⊥AD.
又PA∩AD=A,
所以CE⊥平面PAD.
(2)解 由(1)可知CE⊥AD.
在Rt△ECD中,DE=CD·cos 45°=1,CE=CD·sin 45°=1.
又因为AB=CE=1,AB∥CE,
所以四边形ABCE为矩形.
所以S四边形ABCD=S矩形ABCE+S△ECD=AB·AE+ CE·DE=1×2+
CE·DE=1×2+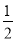 ×1×1=
×1×1=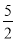 ,
,
又PA⊥平面ABCD,PA=1,
所以V四棱锥P-ABCD=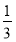 S四边形ABCD·PA=
S四边形ABCD·PA=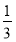 ×
×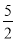 ×1=
×1=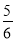 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目