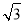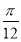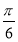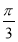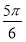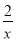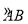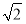题目内容
已知直线l：y＝x＋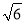
，圆O：x2＋y2＝5，椭圆E：
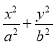＝1(a＞b＞0)的离心率e＝
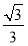，直线l被圆O截得的弦长与椭圆的短轴长相等．
(1)求椭圆E的方程；
(2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两切线的斜率之积为定值．
（1）
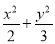＝1.（2）－1
【解析】设椭圆的半焦距为c，
圆心O到直线l的距离d＝
＝
，
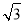∴b＝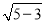
＝
.
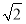由题意得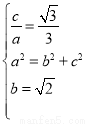
∴a2＝3，b2＝2.
∴椭圆E的方程为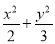＝1.
(2)证明 设点P(x0，y0)，过点P的椭圆E的切线l0的方程为y－y0＝k(x－x0)，
联立直线l0与椭圆E的方程得
消去y得(3＋2k2)x2＋4k(y0－kx0)x＋2(kx0－y0)2－6＝0，
∴Δ＝[4k(y0－kx0)]2－4(3＋2k2)[2(kx0－y0)2－6]＝0，
整理得：(2－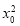
)k2＋2kx0y0－(
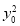－3)＝0，
设满足题意的椭圆E的两条切线的斜率分别为k1，k2，则k1·k2＝－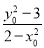
，
∵点P在圆O上，∴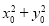
＝5，
∴k1·k2＝－
＝－1.
∴两条切线的斜率之积为常数－1.
练习册系列答案
相关题目
