题目内容
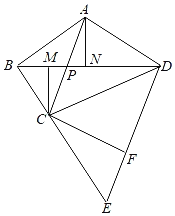
【题目】如图,平面四边形ABCD中,AC与BD交于点P,若3BP=BD,AB=AD![]() BC,
BC,![]() ,则
,则![]() _____.
_____.

【答案】![]()
【解析】
延长BC到E,使得BE=3BC,连结DE,结合已知得![]() 3
3![]() ,由相似三角形性质得P是BD的三等分点,且AP=PC,分别过A,C作BD的垂线,垂足为N,M,PM=PN=BM,得BC=PC,过C作CF//AD交DE于F,则四边形ACFD是平行四边形,设BC=1,计算出各线段长,可得CF⊥DE,四边形ACFD是矩形,这样可计算出
,由相似三角形性质得P是BD的三等分点,且AP=PC,分别过A,C作BD的垂线,垂足为N,M,PM=PN=BM,得BC=PC,过C作CF//AD交DE于F,则四边形ACFD是平行四边形,设BC=1,计算出各线段长,可得CF⊥DE,四边形ACFD是矩形,这样可计算出![]() ,得所求比值.
,得所求比值.
延长BC到E,使得BE=3BC,连结DE,
则![]() 3
3![]() ,又3
,又3![]() 3
3![]() ,
,
∴![]() 3
3![]() ,
,
∴DE//AC,DE=3AP.
∴![]() ,
,
∴![]() ,
,
∴P是BD的三等分点,且AP=PC.
分别过A,C作BD的垂线,垂足为N,M, ∵![]() ,
,
∴PM=PN=BM,
∴BC=PC,
过C作CF//AD交DE于F,则四边形ACFD是平行四边形,
设BC=1,则AB=AD![]() ,CE=2BC=2,CF=AD
,CE=2BC=2,CF=AD![]() ,DE=3PC=3,
,DE=3PC=3,
∴EF![]() DE=1,
DE=1,
∴CE2=CF2+EF2,∴CF⊥DE,
∴四边形ACFD是矩形,∴∠CAD![]() ,
,
∴CD![]() ,
,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目


