题目内容
已知函数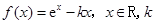 为常数,e是自然对数的底数.
为常数,e是自然对数的底数.
(Ⅰ)当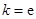 时,证明
时,证明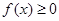 恒成立;
恒成立;
(Ⅱ)若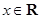 ,且对于任意
,且对于任意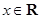 ,
,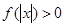 恒成立,试确定实数
恒成立,试确定实数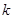 的取值范围.
的取值范围.
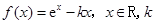 为常数,e是自然对数的底数.
为常数,e是自然对数的底数.(Ⅰ)当
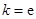 时,证明
时,证明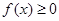 恒成立;
恒成立;(Ⅱ)若
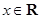 ,且对于任意
,且对于任意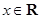 ,
,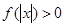 恒成立,试确定实数
恒成立,试确定实数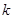 的取值范围.
的取值范围.(Ⅰ)确定函数有最小值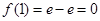 ,所以
,所以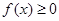 恒成立.
恒成立.
(Ⅱ)实数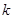 的取值范围是
的取值范围是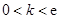 .
.
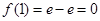 ,所以
,所以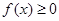 恒成立.
恒成立.(Ⅱ)实数
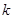 的取值范围是
的取值范围是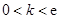 .
.试题分析:(Ⅰ)由
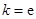 得
得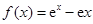 ,所以
,所以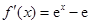 .
.由
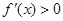 得
得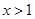 ,故
,故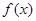 的单调递增区间是
的单调递增区间是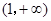 ,
,由
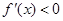 得
得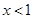 ,故
,故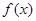 的单调递减区间是
的单调递减区间是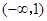 .
.所以函数有最小值
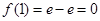 ,所以
,所以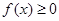 恒成立.
恒成立.(Ⅱ)由
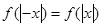 可知
可知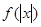 是偶函数.
是偶函数.于是
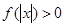 对任意
对任意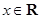 成立等价于
成立等价于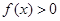 对任意
对任意 成立.
成立.由
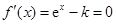 得
得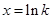 .
.①当
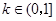 时,
时,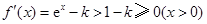 .
.此时
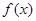 在
在 上单调递增.
上单调递增.故
 ,符合题意.
,符合题意.②当
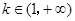 时,
时,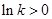 .
.当
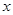 变化时
变化时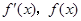 的变化情况如下表:
的变化情况如下表: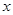 | 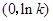 |  | 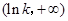 |
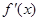 |  |  | 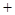 |
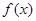 | 单调递减 | 极小值 | 单调递增 |
 上,
上,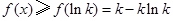 .
.依题意,
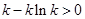 ,又
,又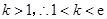 .
.综合①,②得,实数
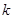 的取值范围是
的取值范围是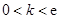 .
.点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。涉及不等式恒成立问题,转化成了研究函数的单调性及最值,得到求证不等式。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
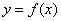 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则 .
.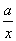 .
.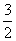 ,求a的值;
,求a的值;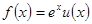 ,
,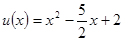 ,求函数
,求函数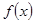 的极小值,
的极小值,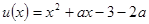 ,设
,设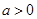 ,函数
,函数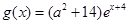 .若存在
.若存在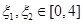 使得
使得 成立,求
成立,求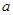 的取值范围.
的取值范围. ,若函数
,若函数 有大于零的极值点,则
有大于零的极值点,则 的取值范围是
的取值范围是 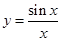 上的点
上的点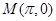 的切线方程为________________。
的切线方程为________________。 ,并设:
,并设: 
 ,
, 至少有3个实根;
至少有3个实根; 当
当 时,方程
时,方程 当
当 时,方程
时,方程



 元(
元( 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价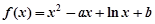
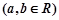 ,
,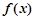 在
在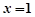 处的切线方程为
处的切线方程为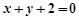 ,求实数
,求实数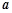 ,
,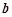 的值;
的值;