题目内容
已知 ,并设:
,并设:

 ,
, 至少有3个实根;
至少有3个实根;
 当
当 时,方程
时,方程 有9个实根;
有9个实根;
 当
当 时,方程
时,方程 有5个实根.
有5个实根.
则下列命题为真命题的是
 ,并设:
,并设: 
 ,
, 至少有3个实根;
至少有3个实根; 当
当 时,方程
时,方程 有9个实根;
有9个实根; 当
当 时,方程
时,方程 有5个实根.
有5个实根.则下列命题为真命题的是
A. | B. | C.仅有 | D. |
A
试题分析:因为,函数
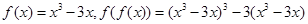
所以,
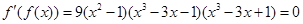 有8个解(4个极大值点,4个极小量值点)
有8个解(4个极大值点,4个极小量值点)极大值=2,极小值=-2,所以,f(f(x))有9个零点。
令f(f(x))=c,当c>2或c<-2时,f(f(x))=c只有一个实根;
当c=2或c=-2时,f(f(x))=c有5个实根;
当-2<c<-2时,f(f(x))=c有9个实根;
所以P:对于任意的c属于R,f(f(x))=c至少有3个实根;假
q:当c属于(-2,2)时,f(f(x))=c有9个实根;真
r:当c=2时,f(f(x))=c有5个实根;真
 是真命题,故选A。
是真命题,故选A。点评:中档题,综合性较强,注意理解“函数f(x)的零点”与“方程f(x)=0的根”,以及应用导数研究函数的方法。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 .
.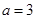 时,求曲线
时,求曲线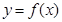 在点
在点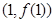 处的切线方程;
处的切线方程;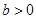 ,
,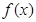 在区间
在区间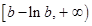 上是增函数,求实数
上是增函数,求实数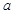 的取值范围.
的取值范围.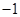 ≤a≤1,
≤a≤1,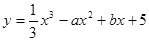 有极值的概率为( )
有极值的概率为( )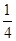
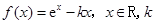 为常数,e是自然对数的底数.
为常数,e是自然对数的底数.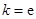 时,证明
时,证明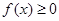 恒成立;
恒成立;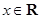 ,且对于任意
,且对于任意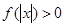 恒成立,试确定实数
恒成立,试确定实数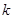 的取值范围.
的取值范围.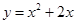 在
在 处的切线的斜率为( )
处的切线的斜率为( )

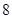
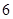
 ,若
,若 在区间
在区间 上单调递减,则
上单调递减,则 的取值范围是C
的取值范围是C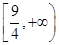



 ,则
,则 等于
等于 

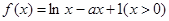
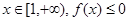 恒成立,求实数
恒成立,求实数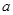 的最小值.
的最小值.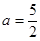 且关于
且关于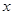 的方程
的方程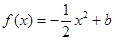 在
在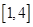 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数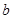 的取值范围;
的取值范围;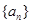 满足:
满足: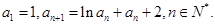 求证:
求证: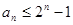
 的导函数
的导函数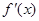 的图象,则下面判断正确的是
的图象,则下面判断正确的是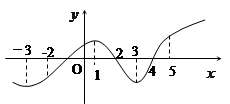
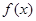 是增函数;
是增函数; 时,
时,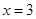 ,
,