题目内容
(2012•香洲区模拟)已知曲线C1的极坐标方程为ρ=6cosθ,曲线C2的极坐标方程为θ=
(ρ∈R),曲线C1、C2相交于点A、B.则弦AB的长等于
| π |
| 4 |
3
| 2 |
3
.| 2 |
分析:先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2及曲线C1的直角坐标方程.再利用直角坐标方程的形式,先求出圆心(3,0)到直线的距离,最后结合点到直线的距离公式弦AB的长度.
解答:解:曲线C2:θ=
(p∈R)表示直线y=x,
曲线C1:P=6cosθ,即p2=6pcosθ
所以x2+y2=6x即(x-3)2+y2=9
∵圆心(3,0)到直线的距离 d=
,
r=3,
∴弦长AB=2
=3
.
∴弦AB的长度 3
.
故答案为:3
.
| π |
| 4 |
曲线C1:P=6cosθ,即p2=6pcosθ
所以x2+y2=6x即(x-3)2+y2=9
∵圆心(3,0)到直线的距离 d=
3
| ||
| 2 |
r=3,
∴弦长AB=2
| r2-d2 |
| 2 |
∴弦AB的长度 3
| 2 |
故答案为:3
| 2 |
点评:本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆心到直线的距等基本方法,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

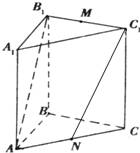 (2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.
(2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.