题目内容

2．已知函数f（x）=$\frac{1}{3}$x3-x2-x+m在[0，1]上的最小值为$\frac{1}{3}$，则实数m的值为2．

分析 求出函数的导数，通过求解极值点，端点的函数求出最小值，然后求解m即可．

解答 解：函数f（x）=$\frac{1}{3}$x3-x2-x+m，
可得f′（x）=x2-2x-1．
令x2-2x-1=0，可得x=1$±\sqrt{2}$，
x∈（1-$\sqrt{2}$，1+$\sqrt{2}$）时，f′（x）＜0，函数是减函数，
x=1时函数取得最小值：可得：$\frac{1}{3}-1-1+m=\frac{1}{3}$，
解得m=2．
故答案为：2．

点评 本题考查函数的导数的应用，函数的最值的求法，考查计算能力．

练习册系列答案
相关题目
12．直线（cos$\frac{π}{6}$）x+（sin$\frac{π}{6}$）y+2=0的倾斜角为（　　）
A．$\frac{π}{6}$B．$\frac{5π}{6}$C．$\frac{π}{3}$D．$\frac{2π}{3}$
13．执行如图所示的程序框图，若“否”箭头分别指向①和②，则输出的结果分别是（　　）
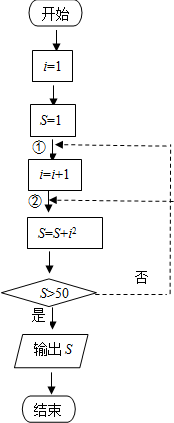
A．55，53B．51，49C．55，49D．53，51
10．若双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的渐近线方程是y=±$\sqrt{2}$x，则双曲线的离心率等于（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．$\frac{{\sqrt{3}}}{3}$
17．函数f（x）=2lnx+$\frac{1}{x}$的单调递减区间是（　　）
A．（-∞，$\frac{1}{2}$]B．（0，$\frac{1}{2}$]C．[$\frac{1}{2}$，1）D．[1，+∞﹚
3．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1（-c，0），F2（c，0），M为椭圆上的一点，且满足∠F1MF2=$\frac{π}{3}$．
（1）求椭圆离心率的取值范围；
（2）当椭圆的离心率e取得最小值时，点N$（0，3\sqrt{3}）$到椭圆上的点的最远距离为4$\sqrt{3}$，求此时椭圆C的方程．
10．下列双曲线中，有一个焦点在抛物线y2=2x准线上的是（　　）
A．6y2-12x2=1B．12x2-6y2=1C．2x2-2y2=1D．4x2-4y2=1
7．若实数x可以在|x+1|≤3的条件下任意取值，则x是负数的概率是$\frac{2}{3}$．
8．下面使用类比推理正确的是（　　）
A．若直线a∥b，b∥c，则a∥c．类比推出：若向量$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$
B．a（b+c）=ab+ac．类比推出：loga（x+y）=logax+logay
C．已知a，b∈R，若方程x2+ax+b=0有实数根，则a2-4b≥0．类比推出：已知a，b∈C，若方程x2+ax+b=0有实数根，则a2-4b≥0．
D．长方形对角线的平方等于长与宽的平方和．类比推出：长方体对角线的平方等于长、宽、高的平方和

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网