题目内容
19.设ABCD为xOy平面的一个正方形,其顶点是A(0,0),B(1,0),C(1,1),D(0,1),u=2xy,v=x2-y2是xOy平面到uOv平面的变换,则正方形ABCD的像(u,v)点集是( )| A. | 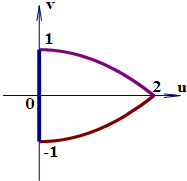 | B. | 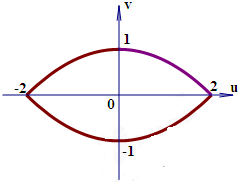 | ||
| C. | 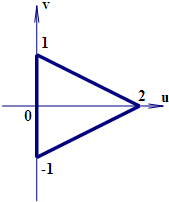 | D. | 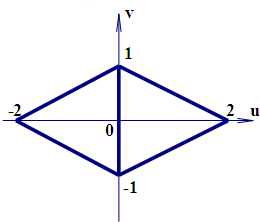 |
分析 由题意,分x与y同号,异号讨论,从而求解.
解答 解:∵A(0,0),B(1,0),C(1,1),D(0,1),
∴①AB的方程为:y=0,(0≤x≤1),
此时u=2xy=0,v=x2-y2=x2∈[0,1],
此时所有的点的轨迹是原点与(0,1)点连接所成的线段;
②BC的方程为:x=1,(0≤y≤1),
此时u=2xy=2y,v=x2-y2=1-y2,
此时v=1-$\frac{1}{4}$u2,
此时所有的点的轨迹是(2,0)与(0,1)点连接所成的抛物线的一部分;
③CD的方程为:y=1,(0≤x≤1),
此时u=2xy=2x,v=x2-y2=x2-1,
此时v=$\frac{1}{4}$u2-1,
此时所有的点的轨迹是(2,0)与(0,-1)点连接所成的抛物线的一部分;
④AD的方程为:x=0,(0≤y≤1),
此时u=2xy=0,v=x2-y2=-y2∈[-1,0],
此时所有的点的轨迹是原点与(0,-1)点连接所成的线段;
综上可得:正方形ABCD的像(u,v)点集是:
故选:A.
点评 本题考查了函数图象的变换,属于基础题

练习册系列答案
相关题目
4.命题p:?x∈R,x2+ax+a2≥0;命题q:若一条直线不在平面内,则这条直线就与这个平面平行,则下列命题中为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | (¬p)∧(¬q) |
11.如图所示,程序框图(算法流程图)输出的结果是( )
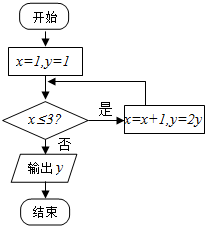

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |