题目内容
（2013•未央区三模）若集合A={x|
≤0}，B={x|x2＜2x}，则A∩B=（ ）
| x |
| x-1 |
分析：分别求解分式不等式和一元二次不等式化简集合A与集合B，然后直接利用交集运算求解．
解答：解：由
≤0，得
，解得0≤x＜1．
所以{x|
≤0}={x|0≤x＜1}，
又B={x|x2＜2x}={x|0＜x＜2}，
所以A∩B={x|0≤x＜1}∩{x|0＜x＜2}={x|0＜x＜1}．
故选A．
| x |
| x-1 |
|
所以{x|
| x |
| x-1 |
又B={x|x2＜2x}={x|0＜x＜2}，
所以A∩B={x|0≤x＜1}∩{x|0＜x＜2}={x|0＜x＜1}．
故选A．
点评：本题考查了交集及其运算，考查了分式不等式及二次不等式的解法，是基础的运算题．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
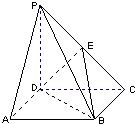（2013•未央区三模）如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．
（2013•未央区三模）某三棱锥的三视图如图所示，该三棱锥的体积是为（ ）