题目内容
已知函数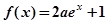 ,
,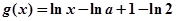 ,其中
,其中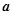 为常数,
为常数,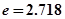 ,函数
,函数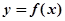 的图象与坐标轴交点处的切线为
的图象与坐标轴交点处的切线为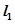 ,函数
,函数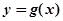 的图象与直线
的图象与直线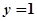 交点处的切线为
交点处的切线为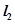 ,且
,且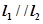 。
。
(Ⅰ)若对任意的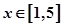 ,不等式
,不等式 成立,求实数
成立,求实数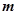 的取值范围.
的取值范围.
(Ⅱ)对于函数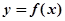 和
和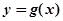 公共定义域内的任意实数
公共定义域内的任意实数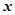 。我们把
。我们把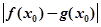 的值称为两函数在
的值称为两函数在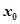 处的偏差。求证:函数
处的偏差。求证:函数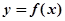 和
和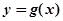 在其公共定义域的所有偏差都大于2.
在其公共定义域的所有偏差都大于2.
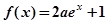 ,
,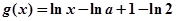 ,其中
,其中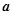 为常数,
为常数,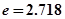 ,函数
,函数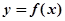 的图象与坐标轴交点处的切线为
的图象与坐标轴交点处的切线为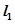 ,函数
,函数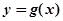 的图象与直线
的图象与直线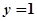 交点处的切线为
交点处的切线为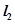 ,且
,且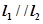 。
。(Ⅰ)若对任意的
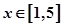 ,不等式
,不等式 成立,求实数
成立,求实数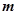 的取值范围.
的取值范围.(Ⅱ)对于函数
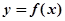 和
和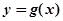 公共定义域内的任意实数
公共定义域内的任意实数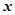 。我们把
。我们把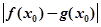 的值称为两函数在
的值称为两函数在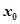 处的偏差。求证:函数
处的偏差。求证:函数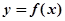 和
和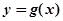 在其公共定义域的所有偏差都大于2.
在其公共定义域的所有偏差都大于2.(Ⅰ)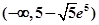 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
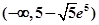 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)利用参数分离法将不等式问题转化为
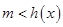 ,等价转化为
,等价转化为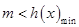 处理,于是问题的核心就是求函数
处理,于是问题的核心就是求函数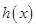 ,利用导数求解,但同时需要注意题中的隐含条件将
,利用导数求解,但同时需要注意题中的隐含条件将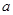 的值确定下来;(Ⅱ)先确定函数
的值确定下来;(Ⅱ)先确定函数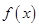 与函数
与函数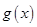 的解析式,然后引入函数
的解析式,然后引入函数 ,通过证明
,通过证明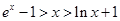 ,进而得到
,进而得到
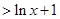 ,得到
,得到 ,于是就说明原结论成立.
,于是就说明原结论成立.试题解析:解(Ⅰ)函数
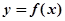 的图象与坐标轴的交点为
的图象与坐标轴的交点为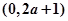 ,
,又

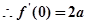
函数
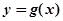 的图象与直线
的图象与直线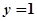 的交点为
的交点为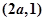 ,
,又
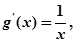
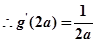
由题意可知,
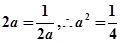
又
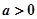 ,所以
,所以 3分
3分不等式
 可化为
可化为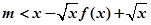
即
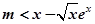
令
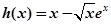 ,则
,则 ,
,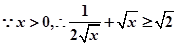
又
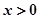 时,
时,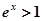 ,
,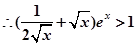 ,
,故
 ,
,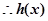 在
在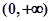 上是减函数
上是减函数即
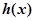 在
在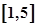 上是减函数
上是减函数因此,在对任意的
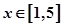 ,不等式
,不等式 成立,
成立,只需

所以实数
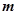 的取值范围是
的取值范围是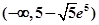 8分
8分(Ⅱ)证明:
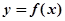 和
和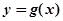 的公共定义域为
的公共定义域为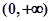 ,由(Ⅰ)可知
,由(Ⅰ)可知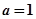 ,
,
令
 ,则
,则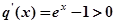 ,
, 在
在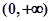 上是增函数
上是增函数故
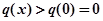 ,即
,即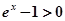 ①
①令
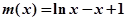 ,则
,则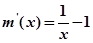 ,
,当
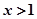 时,
时,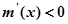 ;当
;当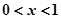 时,
时, ,
,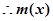 有最大值
有最大值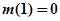 ,因此
,因此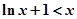 ②
②由①②得
 ,即
,即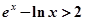
又由①得
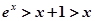
由②得

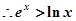
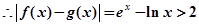
故函数
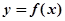 和
和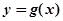 在其公共定义域的所有偏差都大于2 13分
在其公共定义域的所有偏差都大于2 13分
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
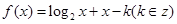 在区间(2,3)上有零点,则
在区间(2,3)上有零点,则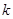 = .
= .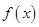 是
是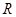 上的单调增函数且为奇函数,数列
上的单调增函数且为奇函数,数列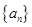 是等差数列,
是等差数列,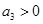 ,则
,则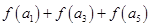 的值( )
的值( )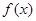 对任意的
对任意的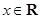 都有
都有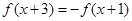 ,且
,且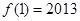 ,则
,则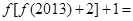 ( )
( )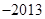
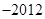
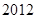
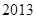
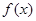 ,若
,若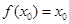 ,则称
,则称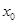 为函数
为函数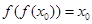 ,则称
,则称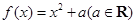 的“稳定点”恰是它的“不动点”,那么实数
的“稳定点”恰是它的“不动点”,那么实数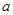 的取值范围是( )
的取值范围是( )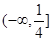
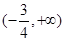
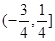
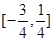
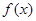 的图象恰好通过
的图象恰好通过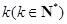 个格点,则称函数
个格点,则称函数 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数: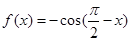 ;②
;②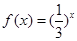 ;③
;③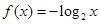 ;④
;④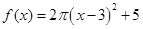 .
.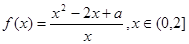 ,其中常数a > 0.
,其中常数a > 0.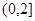 上是减函数;
上是减函数;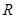 上的函数
上的函数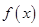 ,满足当
,满足当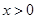 时,
时,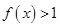 ,且对任意
,且对任意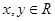 ,有
,有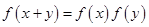 ,
,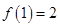
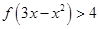
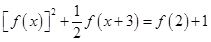
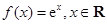 .
. 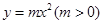 公共点的个数.
公共点的个数. 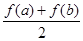 与
与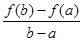 的大小, 并说明理由.
的大小, 并说明理由.