题目内容
【题目】已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(﹣1)=0,且c=1,求f (2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
【答案】(1)9 ; (2)[﹣2,![]() ].
].
【解析】
(1)根据函数f(x)的最小值是f(﹣1)=0,且c=1,求解得a,b,即可求解f (2)的值;
(2)将a=1,c=0代入,|f(x)|≤1在区间(0,1]上恒成立,转化为不等式问题求解即可.
函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)由题意,可得![]() ,a﹣b+1=0,
,a﹣b+1=0,
解得:a=1,b=2;
∴函数f(x)=x2+2x+1.
那么f(2)=4+4+1=9;
(2)由a=1,c=0,可得f(x)=x2+bx;
∵|f(x)|≤1在区间(0,1]上恒成立,
即|x2+bx|≤1
令g(x)=|x2+bx|=|x(x+b)|,显然图象过原点,(b,0).
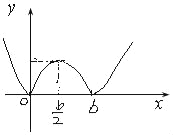
当b<0,g(x)在区间(0,1]上单调递增,可得g(x)的图象,(如图)
g(x)max=g(1)=|b+1|≤1
∴﹣2≤b<0
当b=0时,可得|x2|≤1在区间(0,1]上恒成立,
可得:﹣2≤b≤0;
当b>0,显然g(x)max=![]()
解得:![]() ≥b>0
≥b>0
综上可得b的取值范围是[﹣2,![]() ].
].

练习册系列答案
相关题目