Question

【题目】已知函数（其中），若对任意的，恒成立，则实数的取值范围是________________.

Answer 1

【答案】

【解析】

判断函数f（x）是R上的奇函数，且是增函数；把f（x2+2）+f（﹣2ax）≥0恒成立化为x2+2≥2ax恒成立，设g（x）=x2﹣2ax+2，利用二次函数的图象与性质，即可求出实数a的取值范围．

函数（其中e≈2.718），x∈R；

且f（﹣x）=e﹣x﹣ex+ln（﹣x+）=﹣（ex﹣e﹣x）﹣ln（x+）=﹣f（x），

∴f（x）是R上的奇函数，

又f′（x）=ex+e﹣x+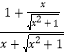＞0恒成立，

∴f（x）是定义域R上的单调增函数；

若对任意的x∈[﹣1，2]，f（x2+2）+f（﹣2ax）≥0恒成立，

∴f（x2+2）≥﹣f（﹣2ax）恒成立，

∴f（x2+2）≥f（2ax）恒成立，

∴x2+2≥2ax恒成立，

即x2﹣2ax+2≥0在x∈[﹣1，2]上恒成立；

设g（x）=x2﹣2ax+2，其对称轴为x=a，且开口向上；

应满足或或；

解得﹣≤a＜-1或或﹣1≤a≤；

∴实数a的取值范围是﹣≤a≤．

故答案为：﹣≤a≤．