题目内容
设 ,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________
,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________
 ,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________
,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________1,6

记

则

因为
 两式相加可得,
两式相加可得,
所以


练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 满足
满足 ,且当
,且当 时,
时, ,则
,则 =( )
=( )

 (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2. ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[ ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.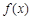 的定义域为
的定义域为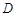 ,若存在非零实数
,若存在非零实数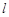 使得对于任意
使得对于任意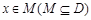 ,有
,有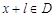 ,且
,且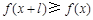 ,则称
,则称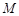 上的
上的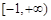 的函数
的函数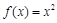 为
为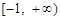 上的
上的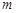 高调函数,那么实数
高调函数,那么实数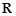 的函数
的函数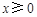 时,
时,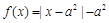 ,且
,且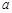 的取值范围是 .
的取值范围是 .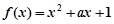 图象上一点
图象上一点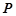 到直线
到直线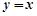 的距离的最小值为
的距离的最小值为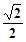 ,则
,则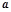 的值为 ▲ .
的值为 ▲ .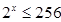 且
且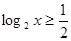 ,
,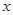 的取值范围;
的取值范围;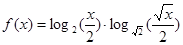 的最大值和最小值。
的最大值和最小值。 种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一 年
种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一 年 的管理费(即销售100元要征收
的管理费(即销售100元要征收 元),于是该产品定价每件比第一年 增加了
元),于是该产品定价每件比第一年 增加了 元,预计年销售量减少
元,预计年销售量减少



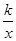 +
+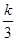 在(1,+∞)上是增函数,则实数k的取值范围是 ( )
在(1,+∞)上是增函数,则实数k的取值范围是 ( )