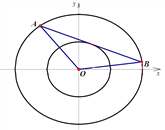
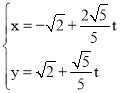题目内容
【题目】已知椭圆C:![]() 1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
(1)求椭圆C的标准方程;
(2)求椭圆C上的点到直线l:4x﹣5y+40=0的最小距离?
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)根据题意列出方程组,求出![]() ,
,![]() ,
,![]() ,从而求出椭圆的标准方程.
,从而求出椭圆的标准方程.
(2)由题可知直线![]() 与椭圆不相交,将直线
与椭圆不相交,将直线![]() 平移,可知其与椭圆相切时,切点到直线
平移,可知其与椭圆相切时,切点到直线![]() 的距离最小或最大,据此可设直线
的距离最小或最大,据此可设直线![]() 平行于直线
平行于直线![]() ,将之与椭圆方程联立,进而得解.
,将之与椭圆方程联立,进而得解.
(1)因为椭圆C上的点到焦点距离的最大值为9,最小值为1,
所以a+c=9,a﹣c=1,
∴a=5,c=4,
∴b2=a2﹣c2=9,
∴椭圆的标准方程为:![]() ;
;
(2)由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交,
设直线m平行于直线l,则直线m的方程可以写成4x﹣5y+k=0,
联立![]() ,整理得25x2+8kx+k2﹣225=0,
,整理得25x2+8kx+k2﹣225=0,
令△=0,得64k2﹣4×25(k2﹣225)=0
解得k1=25或k2=﹣25,
∴当k1=25时,直线m与椭圆交点到直线l的距离最近,
此时直线m的方程为4x﹣5y+25=0,
直线m与直线l间的距离d ,
,
所以,椭圆C上的点到直线l:4x﹣5y+40=0的最小距离是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄 (单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.