题目内容
【题目】椭圆C:![]() 的离心率是
的离心率是![]() ,过焦点且垂直于x轴的直线被椭圆截得的弦长为
,过焦点且垂直于x轴的直线被椭圆截得的弦长为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 过点
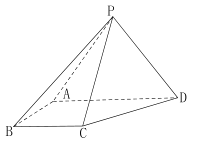
过点![]() 的动直线l与椭圆C相交于A,B两点,在y轴上是否存在异于点P的定点Q,使得直线l变化时,总有
的动直线l与椭圆C相交于A,B两点,在y轴上是否存在异于点P的定点Q,使得直线l变化时,总有![]() ?若存在,求点Q的坐标;若不存在,说明理由.
?若存在,求点Q的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)存在定点
;(2)存在定点![]() 满足题意。
满足题意。
【解析】
(1)利用已知条件![]() ,求解a,b,即可得到椭圆方程.
,求解a,b,即可得到椭圆方程.
(2)当直线l斜率存在时,设直线l方程:y=kx+1,联立直线与椭圆方程,设A,B坐标,假设存在定点Q(0,t)符合题意,利用韦达定理,把![]() 转化为kQA=﹣kQB,求解即可.
转化为kQA=﹣kQB,求解即可.
(1)因为过焦点且垂直于x轴的直线被椭圆截得的弦长为![]() ,得
,得![]() ,且离心率是
,且离心率是![]() ,所以
,所以![]() 得
得![]() ,
,![]() ,所以椭圆C的方程为:
,所以椭圆C的方程为:![]() ;
;
![]() 当直线l斜率存在时,设直线l方程:
当直线l斜率存在时,设直线l方程:![]() ,
,
由![]() 得
得![]() ,
,![]() ,
,
设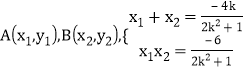 ,
,
假设存在定点![]() 符合题意,
符合题意,![]() ,
,![]() ,
,
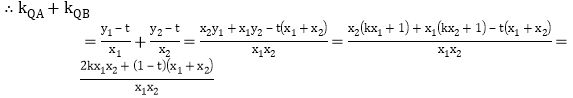
![]() ,
,
![]() 上式对任意实数k恒等于零,
上式对任意实数k恒等于零,![]() ,即
,即![]() ,
,![]() .
.
当直线l斜率不存在时,A,B两点分别为椭圆的上下顶点![]() ,
,![]() ,
,
显然此时![]() ,
,
综上,存在定点![]() 满足题意
满足题意

练习册系列答案
相关题目