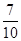题目内容
某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.

(Ⅰ)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(Ⅱ)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(Ⅰ)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(Ⅱ)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
(Ⅰ)6,(Ⅱ)

试题分析:(Ⅰ)根据频率分布直方图中小长方形面积为频率,而频数为总数与频率之积. 因此参加社区服务在时间段
 的学生人数为
的学生人数为 (人),参加社区服务在时间段
(人),参加社区服务在时间段 的学生人数为
的学生人数为 (人).所以参加社区服务时间不少于90小时的学生人数为
(人).所以参加社区服务时间不少于90小时的学生人数为 (人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件
(人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件 .由(Ⅰ)可知,参加社区服务在时间段
.由(Ⅰ)可知,参加社区服务在时间段 的学生有4人,记为
的学生有4人,记为 ;参加社区服务在时间段
;参加社区服务在时间段 的学生有2人,记为
的学生有2人,记为 .从这6人中任意选取2人有
.从这6人中任意选取2人有 共15种情况.事件
共15种情况.事件 包括
包括 共7种情况.所以所选学生的服务时间在同一时间段内的概率
共7种情况.所以所选学生的服务时间在同一时间段内的概率 .
.解:(Ⅰ)由题意可知,
参加社区服务在时间段
 的学生人数为
的学生人数为 (人),
(人),参加社区服务在时间段
 的学生人数为
的学生人数为 (人).
(人).所以参加社区服务时间不少于90小时的学生人数为
 (人). 5分
(人). 5分(Ⅱ)设所选学生的参加服务时间在同一时间段内为事件
 .
.由(Ⅰ)可知,
参加社区服务在时间段
 的学生有4人,记为
的学生有4人,记为 ;
;参加社区服务在时间段
 的学生有2人,记为
的学生有2人,记为 .
.从这6人中任意选取2人有
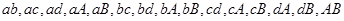 共15种情况.
共15种情况.事件
 包括
包括 共7种情况.
共7种情况.所以所选学生的服务时间在同一时间段内的概率
 . 13分
. 13分
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目



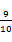
 满足
满足 ,则
,则

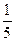

 ,求
,求 有实根的概率为( )
有实根的概率为( )