题目内容
以下命题正确的是______.
①把函数y=3sin(2x+
)的图象向右平移
个单位,得到y=3sin2x的图象;
②一平面内两条直线的方程分别是f1(x,y)=0,f2(x,y)=0,它们的交点是P(x0,y0),则方程f1(x,y)+f2(x,y)=0表示的曲线经过点P;
③由“若ab=ac(a≠0,a,b,c,∈R),则b=c”.类比“若
•
=
•
(
≠
,
,
,
为三个向量),则
=
;
④若等差数列{an}前n项和为sn,则三点(10,
),(100,
),(110,
)共线.
①把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
②一平面内两条直线的方程分别是f1(x,y)=0,f2(x,y)=0,它们的交点是P(x0,y0),则方程f1(x,y)+f2(x,y)=0表示的曲线经过点P;
③由“若ab=ac(a≠0,a,b,c,∈R),则b=c”.类比“若
| a |
| b |
| a |
| c |
| a |
| 0 |
| a |
| b |
| c |
| b |
| c |
④若等差数列{an}前n项和为sn,则三点(10,
| s10 |
| 10 |
| s100 |
| 100 |
| s110 |
| 110 |
①把函数y=3sin(2x+
)的图象向右平移
个单位,得到y=3sin[2(x-
)+
]=3sin2x,∴①正确;
②∵P(x0,y0),是f1(x,y)=0,f2(x,y)=0的交点,∴f1(x0,y0)=0,f2(x0,y0)=0,则方程f1(x0,y0)+f2(x,yx0,y0)=0,即程f1(x,y)+f2(x,y)=0表示的曲线经过点P,∴②正确.
③根据向量的数量积公式可知“若
•
=
•
(
≠
,
,
,
为三个向量),则
=
错误,∴③错误.
④等差数列{an}前n项和为Sn=na1+
d,
∴
=a1+
d=
n+(a1-
),
∴数列{
}关于n的一次函数(d≠0)或常函数(d=0),故三点(10,
),(100,
),(110,
)共线.∴④正确.
故答案为:①②④.
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
②∵P(x0,y0),是f1(x,y)=0,f2(x,y)=0的交点,∴f1(x0,y0)=0,f2(x0,y0)=0,则方程f1(x0,y0)+f2(x,yx0,y0)=0,即程f1(x,y)+f2(x,y)=0表示的曲线经过点P,∴②正确.
③根据向量的数量积公式可知“若
| a |
| b |
| a |
| c |
| a |
| 0 |
| a |
| b |
| c |
| b |
| c |
④等差数列{an}前n项和为Sn=na1+
| n(n-1) |
| 2 |
∴
| Sn |
| n |
| n-1 |
| 2 |
| d |
| 2 |
| d |
| 2 |
∴数列{
| Sn |
| n |
| s10 |
| 10 |
| s100 |
| 100 |
| s110 |
| 110 |
故答案为:①②④.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
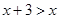 ;
;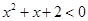 ;④有些三角形不是等边三角形;
;④有些三角形不是等边三角形;