题目内容
(本大题10分)求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
(1)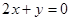 ;(2)
;(2)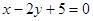 。
。
解析试题分析:先通过两直线方程联立解方程组求出交点坐标.(1)根据两直线平行,斜率相等,设出所求直线方程,将交点坐标代入即可求出平行直线的方程.
(2)根据两直线垂直,斜率之积等于-1,设出所求直线的斜截式方程,然后将交点坐标代入所求直线的方程,即可得解.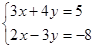 解得
解得 --------2分
--------2分
所以交点(-1,2)
(1)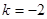 -----4分
-----4分
直线方程为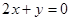 --------6分
--------6分
(2)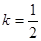 ---------8分
---------8分
直线方程为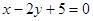 --------10分.
--------10分.
考点:两直线平行与垂直的判定..
点评:两直线平行:斜率都不存在或斜率相等.两直线垂直:斜率之积等于-1或一条直线的斜率不存在,另一条斜率等于0.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
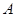 ,
,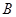 的坐标分别是
的坐标分别是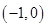 ,
,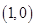 .直线
.直线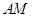 ,
,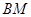 相交于点
相交于点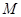 ,且它们的斜率之积为
,且它们的斜率之积为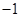 .
.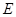 的方程;
的方程;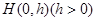 的两直线
的两直线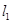 和
和 与轨迹
与轨迹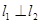 ,求
,求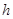 的值;
的值; 轴上是否存在两个定点
轴上是否存在两个定点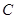 ,
,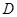 ,使得点
,使得点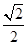 ,若存在,求出定点
,若存在,求出定点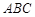 中,点
中,点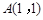 ,
,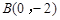 ,
,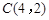 ,
, 为
为 的中点,
的中点,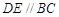 .
. 边上的高所在直线的方程;
边上的高所在直线的方程;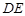 所在直线的方程.
所在直线的方程.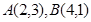 ,直线
,直线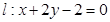 ,在直线
,在直线 上求一点
上求一点 .
.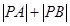 最小; (2)使
最小; (2)使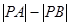 最大.
最大. 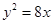 的准线与x轴交于点Q.
的准线与x轴交于点Q. 与抛物线有公共点,求直线
与抛物线有公共点,求直线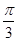 的直线方程;
的直线方程;