题目内容
已知抛物线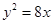 的准线与x轴交于点Q.
的准线与x轴交于点Q.
(Ⅰ)若过点Q的直线 与抛物线有公共点,求直线
与抛物线有公共点,求直线 的斜率的取值范围;
的斜率的取值范围;
(Ⅱ)若过点Q的直线 与抛物线交于不同的两点A、B,求AB中点P的轨迹方程.
与抛物线交于不同的两点A、B,求AB中点P的轨迹方程.
(Ⅰ)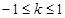 ;(Ⅱ)
;(Ⅱ)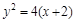 (夹在抛物线
(夹在抛物线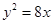 内的部分)。
内的部分)。
解析试题分析:(Ⅰ)由已知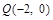 ,直线
,直线 斜率存在,设其方程为
斜率存在,设其方程为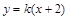 ,
,
由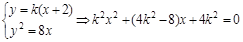 ,故:
,故: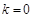 或
或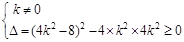
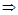
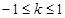 ;
; (Ⅱ)设
(Ⅱ)设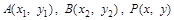 ,则由
,则由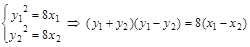 ,
,
∴ 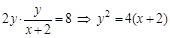 ,
,
即点P的轨迹方程是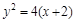 (夹在抛物线
(夹在抛物线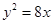 内的部分)。
内的部分)。
考点:本题考查直线与抛物线的位置关系。
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,属于基础题.常需设出直线方程与抛物线方程联立,利用判别式求得问题的答案,但别忘记讨论二次项系数。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
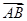 =(4,2).
=(4,2).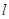 经过直线
经过直线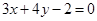 与直线
与直线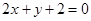 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
. .
.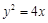 的焦点为F,
的焦点为F,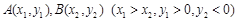 在抛物线上,且存在实数
在抛物线上,且存在实数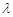 ,使
,使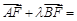
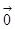 ,
,
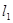 经过点
经过点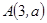 ,
,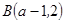 ,直线
,直线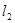 经过点
经过点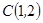 ,
,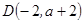 。
。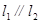 ,求
,求 的值。
的值。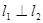 ,求
,求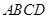 中,边
中,边 所在直线的方程为
所在直线的方程为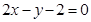 ,点
,点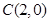 .
.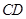 的方程;
的方程; 所在直线的方程.
所在直线的方程.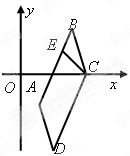
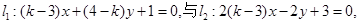 平
平 行
行 已知两点M、N分别在直线
已知两点M、N分别在直线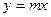 与直线
与直线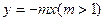 上运动,且|MN|=2.动点P满足
上运动,且|MN|=2.动点P满足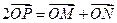 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C.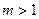 ,都有∠AOB为锐角,求直线l的斜率k的取值范围.
,都有∠AOB为锐角,求直线l的斜率k的取值范围.