题目内容
(本小题12分)已知直线l与两坐标轴围成的三角形的面积为3, 且过定点A(-3,4). 求直线l的方程.
2x+3y-6=0或8x+3y+12=0.
解析试题分析:先分析已知中给出一个点,然后设斜率为k,那么点斜式得到直线的方程,结合面积公式得到结论。
解: 设直线l的方程是y=k(x+3)+4,它在x轴、y轴上的截距分别是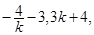
由已知,得|(3k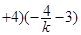 |=6, 解得
|=6, 解得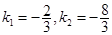 .
.
所以直线l的方程为2x+3y-6=0或8x+3y+12=0.
考点:本题主要考查了直线方程的求解的运用。
点评:解决该试题的关键是能利用已知条件,设点斜式方程,然后结合在两个坐标轴上的截距得到三角形的面积,进而得到k的值。

练习册系列答案
相关题目
 ,B
,B ,C
,C ;
;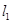 :
: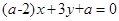 和
和 :
: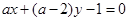 。
。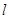 经过直线
经过直线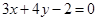 与直线
与直线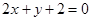 的交点
的交点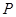 ,且垂直于直线
,且垂直于直线 .
.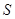 .
.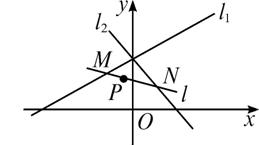
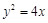 的焦点为F,
的焦点为F,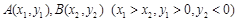 在抛物线上,且存在实数
在抛物线上,且存在实数 ,使
,使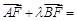
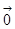 ,
,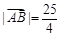
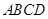 中,边
中,边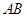 所在直线的方程为
所在直线的方程为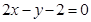 ,点
,点 .
.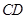 的方程;
的方程; 所在直线的方程.
所在直线的方程.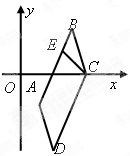
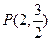 的直线
的直线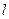 与
与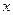 轴的正半轴、
轴的正半轴、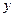 轴的正半轴分别交于点
轴的正半轴分别交于点 、
、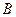 ,
,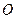 为坐标原点,
为坐标原点,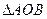 的面积等于6,求直线
的面积等于6,求直线