题目内容
(本小题满分12分)
已知直线l1经过A(1,1)和B(3,2),直线l2方程为2x-4y-3=0.
(1)求直线l1的方程;
(2)判断直线l1与l2的位置关系,并说明理由。
(1)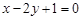 (2)
(2)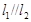 理由:斜率相等,截距不等
理由:斜率相等,截距不等
解析试题分析:(Ⅰ)法一:依题意,直线 的斜率
的斜率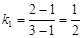 ………2分
………2分
∴ 直线 的方程为
的方程为 ……………4分
……………4分
即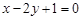 ……………6分
……………6分
法二:∵ 直线 经过点
经过点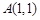 和
和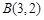
∴ 由两点式方程可知直线 的方程为
的方程为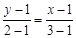 ……………4分
……………4分
即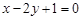 ………….6分
………….6分
法三:设直线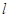 方程为
方程为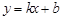 ………………1分
………………1分
将点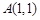 和
和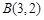 代入上式得……………2分
代入上式得……………2分 ……………4分
……………4分
解得: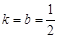 ……………5分
……………5分
∴ 直线 的方程为
的方程为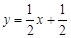 ,即
,即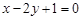 .……………6分
.……………6分
(Ⅱ)直线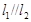 ,下证之………………7分
,下证之………………7分
直线 的方程可化为:
的方程可化为: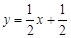 ………………8分
………………8分
∴ 直线 的斜率
的斜率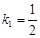 ,在
,在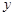 轴上的截距
轴上的截距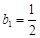 ………………9分
………………9分
直线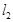 的方程可化为:
的方程可化为: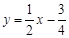 ……………10分
……………10分
∴ 直线 的斜率
的斜率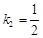 ,在
,在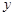 轴上的截距
轴上的截距 ……………11分
……………11分
∴ 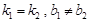 ,故
,故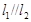 ……………12分
……………12分
考点:直线方程与平面两直线位置关系
点评:两直线平行要满足:斜率相等,截距不等两个条件

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
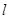 过点P(-2,1),
过点P(-2,1),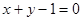 平行,求直线
平行,求直线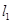 :
: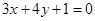 和点
和点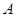 (1,2),设过
(1,2),设过 .
. 垂直,并且与原点的距离是5的直线的方程.
垂直,并且与原点的距离是5的直线的方程.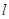 经过直线
经过直线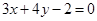 与直线
与直线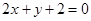 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
.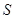 .
.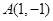 向直线
向直线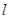 作垂线,垂足为
作垂线,垂足为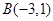 .求直线
.求直线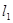 经过点
经过点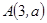 ,
,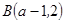 ,直线
,直线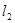 经过点
经过点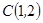 ,
,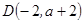 。
。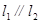 ,求
,求 的值。
的值。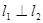 ,求
,求