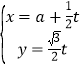题目内容
【题目】已知点P在直线l:y=x-1上,若存在过点P的直线交抛物线
于A,B两点,且|PA|=|AB|,则称点P为“正点”,那么下列结论中正确的是( )
A.直线l上的所有点都是“正点”
B.直线l上仅有有限个点是“正点”
C.直线l上的所有点都不是“正点”
D.直线l上有无穷多个点(但不是所有的点)是“正点”
【答案】A
【解析】
根据题意，设出A，P的坐标，进而B的坐标可表示出，把A，B的坐标代入抛物线方程联立消去y，求得判别式大于0恒成立，可推断出方程有解，进而可推断出直线l上的所有点都符合.
如下图：
根据题意，设A(m,n),P(x0,x0-1), 已知|PA|=|AB| ，则B(2m-x0,2n-x0+1),
∵点A,B在y=x2上,∴
.
∴消去n,整理得关于x0的方程为
∵△=(4m-1)2-4(2m2-1)=8m2-8m+5>0恒成立,即方程恒有实数解,故选A.
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（
元）试销l天，得到如表单价（元）与销量
（册）数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（l）根据表中数据，请建立关于的回归直线方程：
（2）预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？
附：
，
，
，
.
