Question

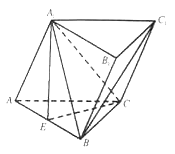
【题目】如图，直三棱柱ABC﹣A′B′C′中，AA′=2AC=2BC，E为AA′的中点，C′E⊥BE．

（1）求证：C′E⊥平面BCE；
（2）求直线AB′与平面BEC′所成角的大小．

Answer 1

【答案】
（1）证明：在矩形ACC′A′中，∵E是AA′的中点，AA′=2AC，

∴EA=AC=EA′=A′C′，

∴∠A′EC′=∠AEC=45°，

∴∠CEC′=90°．即C′E⊥CE．

又C′E⊥BE，CE平面BCE，BE平面BCE，BE∩CE=E，

∴C′E⊥平面BCE

（2）证明：∵C′E⊥平面BCE，BC平面BCE，

∴C′E⊥BC，

又CC′⊥平面ABC，BC平面ABC，

∴CC′⊥BC，又C′E，CC′平面ACC′A′，C′E∩CC′=C′，

∴BC⊥平面ACC′A′，又AC平面ACC′A′，

∴BC⊥AC．

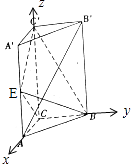
以C为原点，以CA，CB，CC′为坐标轴建立空间直角坐标系如图所示：

设AC=BC=1，则CC′=2．

∴A（1，0，0，），B（0，1，0），B′（0，1，2），E（1，0，1），C′（0，0，2）．

∴ =（﹣1，1，2）， =（1，﹣1，1）， =（0，﹣1，2）．

设平面BC′E的法向量为 =（x，y，z）．则 ．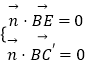

∴ ，令z=1，得 =（1，2，1）．

∴ =3，| |= ，| |= ，

∴cos＜ ＞= = ．

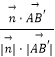∴直线AB′与平面BEC′所成角的正弦值为 ，

∴直线AB′与平面BEC′所成角为30°．

【解析】（1）由△ACE和△A′C′E是等腰直角三角形得∠A′EC′=∠AEC=45°，于是C′E⊥CE，结合C′E⊥BE得出C′E⊥平面BCE；（2）证明BC⊥平面ACC′A′得出AC⊥BC，以C为原点建立空间直角坐标系，设AC=1，求出 和平面BC′E的法向量 ，则直线AB′与平面BEC′所成角的正弦值为|cos＜ ＞|．
【考点精析】通过灵活运用直线与平面垂直的判定和空间角的异面直线所成的角，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则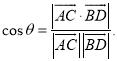即可以解答此题．