题目内容
(5分)(2011•天津)对实数a与b,定义新运算“?”:a?b=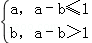 .设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
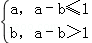 .设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )| A.(﹣1,1]∪(2,+∞) | B.(﹣2,﹣1]∪(1,2] | C.(﹣∞,﹣2)∪(1,2] | D.[﹣2,﹣1] |
B
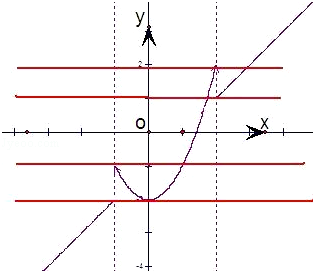
试题分析:根据定义的运算法则化简函数f(x)=(x2﹣2)?(x﹣1),的解析式,并画出f(x)的图象,函数y=f(x)﹣c的图象与x轴恰有两个公共点转化为y=f(x),y=c图象的交点问题,结合图象求得实数c的取值范围.
解:∵
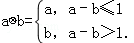 ,
,∴函数f(x)=(x2﹣2)?(x﹣1)
=
 ,
,由图可知,当c∈(﹣2,﹣1]∪(1,2]
函数f(x) 与y=c的图象有两个公共点,
∴c的取值范围是 (﹣2,﹣1]∪(1,2],
故选B.
点评:本题考查二次函数的图象特征、函数与方程的综合运用,及数形结合的思想.属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 的零点个数是__________.
的零点个数是__________. ,集合
,集合 ,
, ,记
,记 分别为集合
分别为集合 中的元素个数,那么下列结论不正确的是( )
中的元素个数,那么下列结论不正确的是( )



 ,若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________.
,若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________. 则方程
则方程 所有实根的个数是( )
所有实根的个数是( )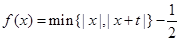 恰有三个零点,则t的值为( ).
恰有三个零点,则t的值为( ).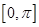 上,关于
上,关于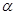 的方程
的方程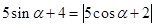 解的个数为 .
解的个数为 .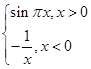 ,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )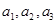 均为正数,
均为正数,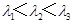 ,则函数
,则函数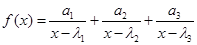 的两个零点分别位于区间( )
的两个零点分别位于区间( )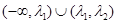 内
内 内
内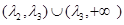 内
内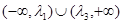 内
内