题目内容
在等差数列{an}中,a2=5,a6=21,记数列{
}的前n项和为Sn,若S2n+1-Sn≤
对n∈N+恒成立,则正整数m的最小值为______.
| 1 |
| an |
| m |
| 15 |
在等差数列{an}中,∵a2=5,a6=21,
∴
,
解得a1=1,d=4,
∴
=
=
,
∵(S2n+1-Sn)-(S2n+3-Sn+1)
=(
+
+…+
)-(
+
+…+
)
=
-
-
=
-
-
=(
-
)+(
-
)>0,
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
数列{S2n+1-Sn}(n∈N*)的最大项为S3-S1=
+
=
,
∵
≤
,∴m≥
,
又∵m是正整数,
∴m的最小值为5.
故答案为:5.
∴
|
解得a1=1,d=4,
∴
| 1 |
| an |
| 1 |
| 1+4(n-1) |
| 1 |
| 4n-3 |
∵(S2n+1-Sn)-(S2n+3-Sn+1)
=(
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n+3 |
=
| 1 |
| an+1 |
| 1 |
| a2n+2 |
| 1 |
| a2n+3 |
=
| 1 |
| 4n+1 |
| 1 |
| 8n+5 |
| 1 |
| 8n+9 |
=(
| 1 |
| 8n+2 |
| 1 |
| 8n+5 |
| 1 |
| 8n+2 |
| 1 |
| 8n+9 |
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
数列{S2n+1-Sn}(n∈N*)的最大项为S3-S1=
| 1 |
| 5 |
| 1 |
| 9 |
| 14 |
| 45 |
∵
| 14 |
| 45 |
| m |
| 15 |
| 14 |
| 3 |
又∵m是正整数,
∴m的最小值为5.
故答案为:5.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
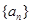 为等比数列,
为等比数列,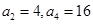 ,记
,记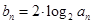 .
.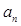 和
和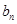 ;
;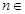
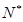 ,有
,有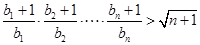 成立.
成立.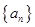 中,
中,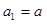 ,
,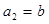 ,
,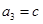 ,
,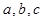 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且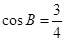 .
.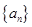 的公比
的公比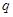 ;
;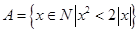 ,且
,且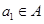 ,求数列
,求数列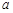 m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.