题目内容

10．设直线l：kx-y+1=0与圆C：x2+y2=4相较于A、B两点，$\overrightarrow{OM}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$，且点M在圆C上，则实数k等于（　　）
A．1B．2C．-1D．0

分析 由已知得四边形OAMB为菱形，弦AB的长为2$\sqrt{3}$，又直线过定点N（0，1），且过N的弦的弦长最小值为2$\sqrt{3}$，由此能求出结果．

解答 解：由题意可得，四边形OAMB为平行四边形，∴四边形OAMB为菱形，
∴△OAM为等边三角形，且边长为2，
解得弦AB的长为2$\sqrt{3}$，又直线过定点N（0，1），
且过N的弦的弦长最小值为2$\sqrt{3}$，
此时此弦平行x轴，即k=0，
故选：D．

点评 本题考查满足条件的实数值的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用，属于基础题．

练习册系列答案
相关题目
20．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，k），且$\overrightarrow{a}$$⊥（2\overrightarrow{a}-\overrightarrow{b}）$，则|$\overrightarrow{b}$|=2$\sqrt{10}$．
1．在等比数列{an}中，a1=2，且a3+a5=40，则{an}的公比q=（　　）
A．±5B．±4C．$±\sqrt{5}$D．±2
18．i为虚数单位，则${（{\frac{1+i}{1-i}}）^7}$=-i．
5．△ABC中，内角A，B，C的对边分别为a，b，c，且cos2A=3cos（B+C）+1．
（Ⅰ）求角A的大小；
（Ⅱ）若cosBcosC=-$\frac{1}{8}$，且△ABC的面积为2$\sqrt{3}$，求a．
15．已知命题p：设a，b∈R，则“a+b＞4”是“a＞2且b＞2”的必要不充分条件；
命题q：“?x0∈R，使得x02-x0＞0”的否定是：“?x∈R，均有x2-x＜0”；
在命题①p∧q；②（?p）∨（?q）；③p∨（?q）； ④（?p）∨q中，真命题的序号是（　　）
A．①③B．①④C．②③D．②④
1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的中心为坐标原点，离心率e=$\frac{\sqrt{6}}{3}$，A1，A2，B1，B2是其四个顶点，且四边形A1B1A2B2的面积为4$\sqrt{3}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过椭圆C的右焦点F且与椭圆C相交于M，N两点的直线l，使得在直线x=3上可以找到一点B，满足△MNB为正三角形？若存在，求出直线l的方程；若不存在，请说明理由．
18．在如图所示的程序框图中，若输出的S值等于16，则在该程序框图中的判断框内填写的条件为（　　）
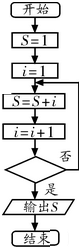
A．i＞5B．i＞6C．i＞7D．i＞8
19．某校乒乓球队男运动员10名和女运动员9名，若要选出男、女运动员各3名参加三场混合双打比赛（每名运动员只限参加一场比赛），共有多少种参赛方法？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网