题目内容
等差数列{am}的前m项和为Sm,已知S3= ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,
(1)求数列{am}的通项公式.
(2)若{am}又是等比数列,令bm= ,求数列{bm}的前m项和Tm.
,求数列{bm}的前m项和Tm.
(1)am=3或am="2m-1" (2)Tm=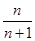
解析试题分析:(1)首先根据等差数列的性质,把已知条件转化为关于a2的方程,解出a2的值,然后再根据等比数列的性质,结合已知条件列出关于a2、d的方程,求出公差d即可求出通项公式;(2)
试题解析:(1)设数列{am}的公差为d,由S3= ,可得3a2=
,可得3a2= ,解得a2=0或a2=3.
,解得a2=0或a2=3.
由S1,S2,S4成等比数列,可得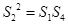 ,由
,由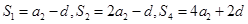 ,故
,故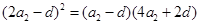 .
.
若a2=0,则 ,解得d=0.此时Sm=0.不合题意;
,解得d=0.此时Sm=0.不合题意;
若a2=3,则 ,解得d=0或d=2,此时am=3或am=2m-1.
,解得d=0或d=2,此时am=3或am=2m-1.
(2)若{am}又是等比数列,则Sm=3m,所以bm= =
=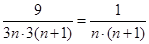 =
=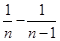 ,
,
故Tm=(1- )+(
)+( -
- )+(
)+( -
-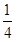 )+…+(
)+…+(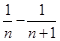 )=1-
)=1-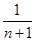 =
=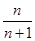 .
.
考点:1.等差数列和等比数列的性质以及等差数列的通项公式;2.数列的前m项和求法—裂项法.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
 ,
,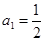 ,且满足
,且满足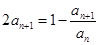 .
. 是等差数列;
是等差数列;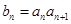 ,求数列
,求数列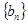 的前n项和
的前n项和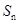 .
.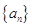 的前
的前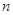 项和为
项和为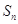 ,
,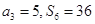 .
. 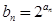 ,求数列
,求数列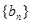 的前
的前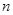 项和
项和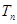 .
.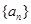 的前
的前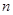 项和为
项和为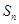 ,已知对任意的
,已知对任意的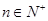 ,点
,点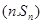 均在函数
均在函数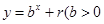 且
且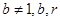 均为常数)的图像上.
均为常数)的图像上.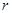 的值;
的值;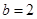 时,记
时,记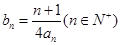 ,求数列
,求数列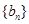 的前
的前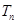 .
.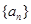 的前
的前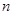 项和为
项和为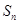 ,且
,且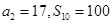 .
.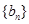 满足
满足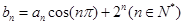 ,求数列
,求数列 的前
的前 项和是
项和是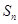 且
且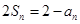
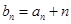 ,求数列
,求数列 的前
的前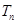 .
.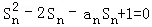 ,n=1,2,3
,n=1,2,3 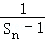 }是等差数列;
}是等差数列; ,数列
,数列 前
前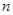 项和
项和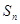 ,
,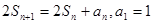 ,数列
,数列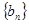 ,满足
,满足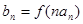 .(Ⅰ)求数列
.(Ⅰ)求数列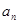 ;
;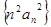 的前
的前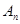 ,数列
,数列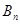 ,证明:
,证明: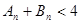 。
。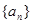 是各项都为正数的等比数列,
是各项都为正数的等比数列, 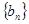 是等差数列,且
是等差数列,且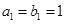 ,
,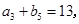
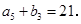
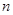 项和为
项和为 ,求数列
,求数列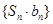 的前
的前 .
.