题目内容
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G、F分别是线段CE、PB的中点.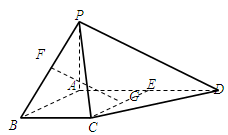
(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求二面角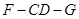 的正切值.
的正切值.
(Ⅰ)详见解析;(Ⅱ)二面角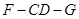 的正切值为
的正切值为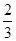 .
.
解析试题分析:(Ⅰ)连结BD,因为E是AD的中点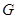 是CE的中点,所以BD过
是CE的中点,所以BD过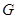 点,这样只需证
点,这样只需证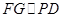 即可;(Ⅱ)求二面角
即可;(Ⅱ)求二面角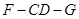 的正切值,需找出平面角,注意到PA⊥平面ABCD,F是线段PB的中点,取
的正切值,需找出平面角,注意到PA⊥平面ABCD,F是线段PB的中点,取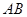 的中点
的中点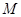 ,则
,则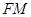 ⊥平面ABCD,过
⊥平面ABCD,过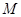 作
作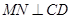 ,垂足为
,垂足为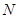 ,则
,则 即为二面角
即为二面角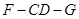 的平面角.
的平面角.
试题解析:(Ⅰ)证明:连结 ,因为E是AD的中点,
,因为E是AD的中点,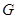 是CE的中点,且ABCE为菱形,
是CE的中点,且ABCE为菱形,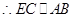 ,
,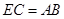 ,所以
,所以 过
过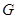 点,且
点,且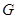 是
是 的中点,在
的中点,在 中,又因为
中,又因为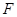 是
是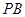 的中点,
的中点, ,又
,又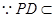 平面
平面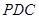 ,
, 平面
平面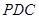 ;
;
(Ⅱ)取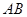 的中点
的中点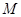 ,因为
,因为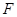 是
是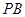 的中点,
的中点,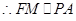 ,又因为
,又因为 平面
平面 ,
,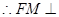 平面
平面 ,过
,过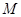 作
作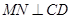 ,垂足为
,垂足为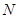 ,连结
,连结 ,则
,则 即为二面角
即为二面角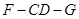 的平面角,
的平面角,
不妨令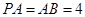 ,则
,则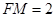 ,有平面几何知识可知
,有平面几何知识可知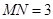 ,
,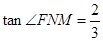 ,所以二面角
,所以二面角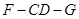 的正切值为
的正切值为 .
.
考点:1、线面平行的判定,2、二面角的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
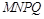 为平行四边形;
为平行四边形;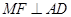 .
.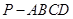 中,侧面
中,侧面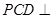 底面
底面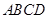 ,
,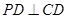 ,
, 为
为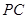 中点,底面
中点,底面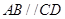 ,
,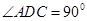 ,
,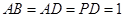 ,
, .
.
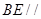 面
面 ;
;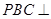 面
面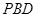 ;
;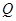 为棱
为棱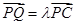 ,试确定
,试确定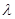 的值使得二面角
的值使得二面角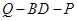 为
为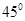 .
.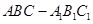 中,
中,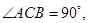
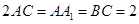 ,
,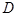 为
为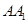 的中点
的中点
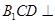 平面
平面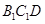 ;
; 到平面
到平面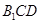 的距离.
的距离.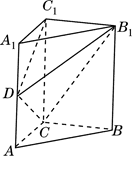
 中,
中, 平面
平面 .
.
 的充分条件,并给予证明;
的充分条件,并给予证明; ,②
,② ;③
;③ 为锐角,求平面
为锐角,求平面 与平面
与平面 所成锐二面角
所成锐二面角 的取值范围.
的取值范围.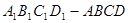 中,
中, ,
,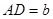 ,
,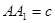 ,
, 是线段
是线段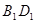 的中点.
的中点.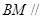 平面
平面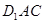 ;
;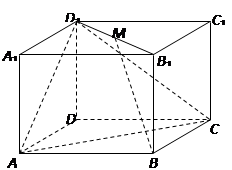
 ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点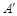 ,连结A¢B.
,连结A¢B.
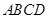 中,
中, 是
是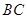 的中点,
的中点, ,
,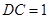 ,
,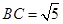 ,
,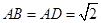 ,将左图沿直线
,将左图沿直线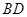 折起,使得二面角
折起,使得二面角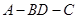 为
为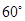 ,如右图.
,如右图.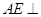 平面
平面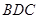 ;
;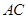 与平面
与平面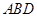 所成角的余弦值.
所成角的余弦值.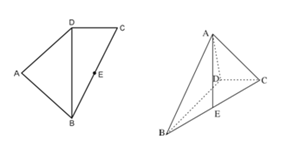
 中,
中, ,
, ,
, 分别为
分别为 的中点.
的中点.
 ;
; .
.