题目内容
如图,直三棱柱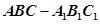 中,
中,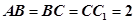 ,
,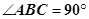 ,D是AC的中点.
,D是AC的中点.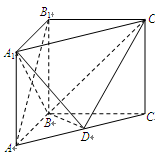
(Ⅰ)求证: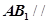 平面
平面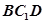 ;
;
(Ⅱ)求几何体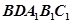 的体积.
的体积.
(Ⅰ)详见解析; (Ⅱ)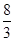 .
.
解析试题分析:(Ⅰ)利用线线平行证明线面平行,抓住直线PD∥B1A达到证明AB1∥平面BC1D;(Ⅱ)采用体积分割技巧,将所求的几何体转化为直三棱柱的体积简单两个三棱锥的体积.
试题解析:(Ⅰ)连接B1C交BC1于点P,连接PD.
由于BB1C1C是平行四边形,所以P为为B1C的中点
因为D为AC的中点,所以直线PD∥B1A,
又PDÌ平面B1CD,B1AË平面BC1D,
所以AB1∥平面BC1D. 6分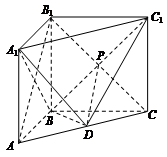
(Ⅱ)直三棱柱ABC-A1B1C1的体积V1=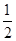 ×2×2×2=4.
×2×2×2=4.
三棱锥C1-BDC的体积V2与三棱锥A1-BDA的体积V3相等,
V2=V3=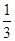 ×
×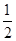 ×
×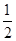 ×2×2×2=
×2×2×2=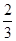 .
.
所以几何体BDA1B1C1的体积V=V1-V2-V3=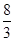 . 12分
. 12分
考点:1.平行关系的证明与判断;2.几何体的体积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
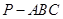 中,
中,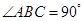 ,
,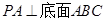
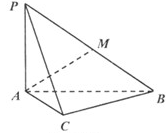
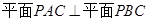 ;
;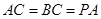 ,
,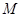 是
是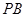 的中点,求
的中点,求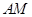 与平面
与平面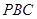 所成角的正切值
所成角的正切值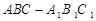 的底面是直角三角形,
的底面是直角三角形, 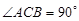 ,侧棱与底面所成角为
,侧棱与底面所成角为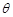 ,点
,点 在底面上的射影
在底面上的射影 落在
落在 上.
上.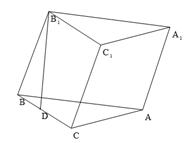
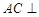 平面
平面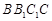 ;
;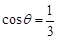 ,且当
,且当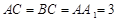 时,求二面角
时,求二面角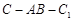 的大小.
的大小.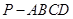 中,侧面
中,侧面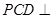 底面
底面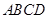 ,
,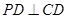 ,
, 为
为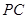 中点,底面
中点,底面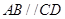 ,
,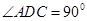 ,
,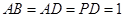 ,
,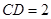 .
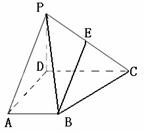
.
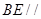 面
面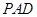 ;
;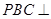 面
面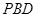 ;
;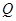 为棱
为棱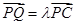 ,试确定
,试确定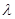 的值使得二面角
的值使得二面角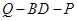 为
为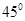 .
. 、
、 为圆柱
为圆柱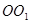 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 、
、 分别是
分别是 的中点,
的中点,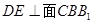 .
.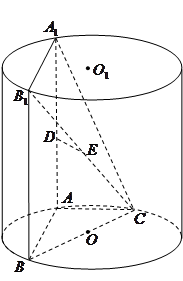
 ;
; ;
;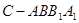 与圆柱
与圆柱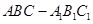 中,
中,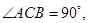
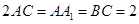 ,
,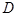 为
为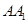 的中点
的中点
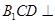 平面
平面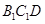 ;
; 到平面
到平面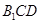 的距离.
的距离.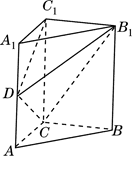
 中,
中, 平面
平面 .
.
 的充分条件,并给予证明;
的充分条件,并给予证明; ,②
,② ;③
;③ 为锐角,求平面
为锐角,求平面 与平面
与平面 所成锐二面角
所成锐二面角 的取值范围.
的取值范围. ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点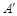 ,连结A¢B.
,连结A¢B.
 的边长为2,
的边长为2, 分别为边
分别为边 的中点,
的中点, 是线段
是线段 的中点,如图,把正方形沿
的中点,如图,把正方形沿 .
.
 取何值,
取何值, 与
与 不可能垂直;
不可能垂直; 的大小为
的大小为 ,当
,当 时,求
时,求 的值.
的值.