题目内容
【题目】如图，已知过原点O的直线与函数
的图象交于A，B两点，分别过A，B作y轴的平行线与函数
图象交于C，D两点，若
轴，则四边形ABCD的面积为_____．
【答案】
【解析】
分析：设出A、B的坐标，求出OA、OB的斜率相等利用三点共线得出A、B的坐标之间的关系．再根据BC平行x轴，B、C纵坐标相等，推出横坐标的关系，结合之前得出A、B的坐标之间的关系即可求出A的坐标，从而解出B、C、D的坐标，最后利用梯形的面积公式求解即可．
详解：设点A、B的横坐标分别为x1、x2由题设知，x1＞1，x2＞1．
则点A、B纵坐标分别为log8x1、log8x2．
因为A、B在过点O的直线上，所以
点C、D坐标分别为（x1，log2x1），（x2，log2x2）．
由于BC平行于x轴知log2x1=log8x2，即得log2x1=
log2x2，∴x2=x13．
代入x2log8x1=x1log8x2得x13log8x1=3x1log8x1．
由于x1＞1知log8x1≠0，∴x13=3x1．考虑x1＞1解得x1=
．
于是点A的坐标为（，log8）即A（，
log23）
∴B（3，
log23），C（，log23），D（3，
log23）．
∴梯形ABCD的面积为S=（AC+BD）×BC=（ log23+log23）×2=
log23．
故答案为：log23
练习册系列答案
相关题目
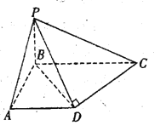
【题目】在如图所示的多面体中，
平面
，
平面，
，且
，
是
的中点．
（
）求证：
．
（
）若
为线段
上一点，且
，求证：
平面
．
（
）在棱
上是否存在一点
，使得直线
与平面所成的角为
．若存在，指出点的位置；若不存在，请说明理由．
