题目内容
14.求下列定积分:(1)${∫}_{\frac{π}{6}}^{\frac{π}{2}}$cos2xdx;
(2)${∫}_{-1}^{2}$|x2-x|dx.
分析 (1)由和的积分等于积分的和展开,然后求出被积函数的原函数,直接由微积分基本定理得答案;
(2)把积分区间分段,取绝对值,然后求出被积函数的原函数,再由微积分基本定理得答案.
解答 解:(1)${∫}_{\frac{π}{6}}^{\frac{π}{2}}$cos2xdx=${∫}_{\frac{π}{6}}^{\frac{π}{2}}$$\frac{1+cos2x}{2}$dx
=${∫}_{\frac{π}{6}}^{\frac{π}{2}}$$\frac{1}{2}$dx+${∫}_{\frac{π}{6}}^{\frac{π}{2}}$$\frac{1}{2}$cos2xdx
=($\frac{1}{2}$x)${|}_{\frac{π}{6}}^{\frac{π}{2}}$+($\frac{1}{4}$sin2x)${|}_{\frac{π}{6}}^{\frac{π}{2}}$
=$\frac{π}{6}-\frac{\sqrt{3}}{8}$;
(2)${∫}_{-1}^{2}$|x2-x|dx
=${∫}_{-1}^{0}$(x2-x)dx+${∫}_{0}^{1}$(x-x2)dx+${∫}_{1}^{2}$(x2-x)dx
=($\frac{1}{3}$x3-$\frac{1}{2}$x2)${|}_{-1}^{0}$+($\frac{1}{2}$x2-$\frac{1}{3}$x3)${|}_{0}^{1}$+($\frac{1}{3}$x3-$\frac{1}{2}$x2)${|}_{1}^{2}$
=$\frac{11}{6}$.
点评 本题考查了定积分,考查了微积分基本定理,是基础的计算题.

练习册系列答案
相关题目
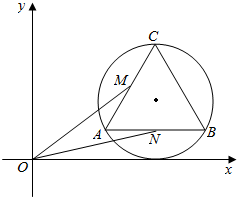 如图,在直角坐标系中,△ABC是以(2,1)为圆心,1为半径的圆的内接正三角形,M、N分别是边AC、AB的中点,$\overrightarrow{OM}$•$\overrightarrow{ON}$的取值范围是[$\frac{39-4\sqrt{5}}{8}$,$\frac{39+4\sqrt{5}}{8}$].
如图,在直角坐标系中,△ABC是以(2,1)为圆心,1为半径的圆的内接正三角形,M、N分别是边AC、AB的中点,$\overrightarrow{OM}$•$\overrightarrow{ON}$的取值范围是[$\frac{39-4\sqrt{5}}{8}$,$\frac{39+4\sqrt{5}}{8}$].