题目内容
3．若实数x，y∈[1，4]，则xy≥$\frac{5}{2}$的概率为1-$\frac{5}{18}ln\frac{5}{2}$．分析 根据积分的应用求出不等式对应的区域的面积，根据几何概型的概率公式进行求解即可．
解答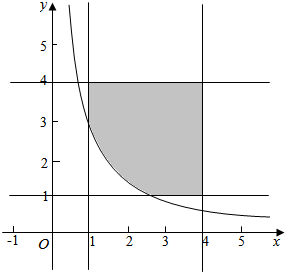 
解：不等式xy≥$\frac{5}{2}$，即y≥$\frac{5}{2x}$对应的平面区域如图
则阴影部分的面积S=3×3-${∫}_{1}^{\frac{5}{2}}\frac{5}{2x}dx$=9-$\frac{5}{2}lnx{|}_{1}^{\frac{5}{2}}$=9-$\frac{5}{2}ln\frac{5}{2}$，
则对应的概率为$\frac{9-\frac{5}{2}ln\frac{5}{2}}{9}$=1-$\frac{5}{18}ln\frac{5}{2}$．
故答案为：1-$\frac{5}{18}ln\frac{5}{2}$．
点评 本题主要考查几何概型的概率的计算，根据积分的应用求出对应的区域面积是解决本题的关键．
练习册系列答案
相关题目
18．在锐角△ABC中，若C=2B，则$\frac{c}{b}$的范围是（ ）
| A． | （0，2） | B． | $（\sqrt{2}，2）$ | C． | $（\sqrt{2}，\sqrt{3}）$ | D． | $（1，\sqrt{3}）$ |
12．一只小蜜蜂在一个棱长为3的正方体内自由飞行，若蜜蜂在飞行过程中始终保持与正方体8个顶点的距离均大于1，称其为“安全飞行”，用蜜蜂“安全飞行”的概率为（ ）
| A． | 1-$\frac{2π}{81}$ | B． | $\frac{2π}{81}$ | C． | 1-$\frac{4π}{81}$ | D． | $\frac{4π}{81}$ |