题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,A1B1⊥A1C1,D是B1C1的中点,A1A=A1B1=2.

(1)求证:AB1∥平面A1CD;
(2)若异面直线AB1和BC所成角为60°,求四棱锥A1﹣CDB1B的体积.
【答案】(1)证明见解析(2)2
【解析】
(1)连AC1交A1C于点E,连DE.证明DE∥AB1,然后证明AB1∥平面A1CD;
(2)∠C1DE或其补角为异面直线AB1和BC所成角,可得 A1D⊥平面CDB1B,求出四棱锥的底面积与高,即可求解体积.
(1)证明:如图,连AC1交A1C于点E,连DE.
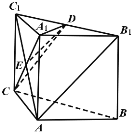
因为直三棱柱ABC﹣A1B1C1中,四边形AA1C1C是矩形,故点E是AC1中点,
又D是B1C1的中点,故DE∥AB1,
又AB1平面A1CD,DE平面A1CD,故AB1∥平面A1CD.
(2)由(1)知DE∥AB1,又C1D∥BC,故∠C1DE或其补角为异面直线AB1和BC所成角.
设AC=2m,则![]() ,
,
故△C1DE为等腰三角形,故∠C1DE=60°,故△C1DE为等边三角形,则有![]() ,得到m=1.
,得到m=1.
故△A1B1C1为等腰直角三角形,故A1D⊥C1B1,
又B1B⊥平面A1B1C1,A1D平面A1B1C1,故A1D⊥B1B,
又B1B∩C1B1=B1,故A1D⊥平面CDB1B,
又梯形CDB1B的面积![]() ,
,
则四棱锥A1﹣CDB1B的体积![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目