题目内容
在直角坐标系xOy中，直线l的方程为x﹣y+4=0，曲线C的参数方程为
（α为参数）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
），判断点P与直线l的位置关系；
（2）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
(1)点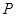
在直线
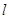上；（2)
.
解析试题分析：(1)将参数方程转化为直角坐标系下的普通方程；（2）掌握常见的将参数方程转化为直角坐标系下的普通方程;(3)解决直线和椭圆的综合问题时注意：第一步：根据题意设直线方程，有的题设条件已知点，而斜率未知；有的题设条件已知斜率，点不定，可由点斜式设直线方程.第二步：联立方程：把所设直线方程与椭圆的方程联立，消去一个元，得到一个一元二次方程.第三步：求解判别式
：计算一元二次方程根.第四步：写出根与系数的关系.第五步：根据题设条件求解问题中结论.（4）根据题意设点根据点到直线的距离公式.
试题解析：解：（I）把极坐标系下的点（4，）化为直角坐标，得P（0，4）．
因为点P的直角坐标（0，4）满足直线l的方程x﹣y+4=0，
所以点P在直线l上．（5分）
（II）设点Q的坐标为（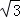
cosα，sinα），
则点Q到直线l的距离为d=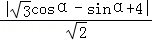
=
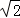cos（
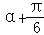）+2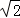
由此得，当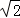cos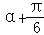（）=﹣1时，d取得最小值，且最小值为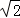．10分
考点：(1)参数方程的应用；（2）点到直线点的距离公式应用.
练习册系列答案
阅读快车系列答案
相关题目
轴的正半轴重合，且长度单位相同．直线
的极坐标方程为：
，曲线C：
（
为参数），其中
．
中，已知曲线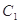
: 
，在极坐标系（与平面直角坐标系
为极点，以
轴正半轴为极轴）中，直线
的极坐标方程为
.
倍、
倍后得到曲线
，试写出直线
，使点
轴正半轴．已知曲线
的极坐标方程为
，曲线
的参数方程为
（其中
为参数）
的直角坐标方程和曲线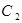
的普通方程；
中，以
为极点，
轴非负半轴为极轴建立坐标系，已知曲线
的极坐标方程为
，直线
的参数方程为: 
（
为参数），两曲线相交于
两点. 求：
求
的值.
的直角坐标方程为
. 以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系. P是曲线
，
，将点P绕点O逆时针旋转角
后得到点Q，
，点M的轨迹是曲线
.
的取值范围.
且与极轴垂直的直线交曲线
于
、
两点，则
. 
，点B在直线
上运动，当线段AB最短时，点B的极坐标为__________。
到直线ρsinθ＝2的距离．