题目内容
【题目】已知函数![]() ,
,![]() 图象上两相邻对称轴之间的距离为
图象上两相邻对称轴之间的距离为![]() ;_______________;
;_______________;
(Ⅰ)在①![]() 的一条对称轴
的一条对称轴![]() ;②
;②![]() 的一个对称中心
的一个对称中心![]() ;③
;③![]() 的图象经过点
的图象经过点![]() 这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
(Ⅱ)若动直线![]() 与
与![]() 和
和![]() 的图象分别交于
的图象分别交于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最大值及此时
长度的最大值及此时![]() 的值.
的值.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(Ⅰ)选①或②或③,![]() ;(Ⅱ)当
;(Ⅱ)当![]() 或
或![]() 时,线段
时,线段![]() 的长取到最大值
的长取到最大值![]() .
.
【解析】
(Ⅰ)先根据题中信息求出函数![]() 的最小正周期,进而得出
的最小正周期,进而得出![]() .
.
选①,根据题意得出![]() ,结合
,结合![]() 的取值范围可求出
的取值范围可求出![]() 的值,进而得出函数
的值,进而得出函数![]() 的解析式;
的解析式;
选②,根据题意得出![]() ,结合
,结合![]() 的取值范围可求出
的取值范围可求出![]() 的值,进而得出函数
的值,进而得出函数![]() 的解析式;
的解析式;
选③,根据题意得出![]() ,结合
,结合![]() 的取值范围可求出
的取值范围可求出![]() 的值,进而得出函数
的值,进而得出函数![]() 的解析式;
的解析式;
(Ⅱ)令![]() ,利用三角恒等变换思想化简函数
,利用三角恒等变换思想化简函数![]() 的解析式,利用正弦型函数的基本性质求出
的解析式,利用正弦型函数的基本性质求出![]() 在
在![]() 上的最大值和最小值,由此可求得线段
上的最大值和最小值,由此可求得线段![]() 长度的最大值及此时
长度的最大值及此时![]() 的值.
的值.
(Ⅰ)由于函数![]() 图象上两相邻对称轴之间的距离为
图象上两相邻对称轴之间的距离为![]() ,则该函数的最小正周期为
,则该函数的最小正周期为![]() ,
,![]() ,此时
,此时![]() .
.
若选①,则函数![]() 的一条对称轴
的一条对称轴![]() ,则
,则![]() ,
,
得![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
此时,![]() ;
;
若选②,则函数![]() 的一个对称中心
的一个对称中心![]() ,则
,则![]() ,
,
得![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
此时,![]() ;
;
若选③,则函数![]() 的图象过点
的图象过点![]() ,则
,则![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,此时,
,此时,![]() .
.
综上所述,![]() ;
;
(Ⅱ)令![]()
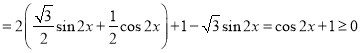 ,
,![]() ,
,
![]() ,
,![]() ,当
,当![]() 或
或![]() 时,即当
时,即当![]() 或
或![]() 时,
时,
线段![]() 的长取到最大值
的长取到最大值![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目