题目内容
【题目】已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=![]() (n∈N*)
(n∈N*)
(Ⅰ)证明当n≥2时,数列{nan}是等比数列,并求数列{an}的通项an;
(Ⅱ)求数列{n2an}的前n项和Tn;
(Ⅲ)对任意n∈N*,使得![]() 恒成立,求实数λ的最小值.
恒成立,求实数λ的最小值.
【答案】(Ⅰ) (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ) ![]()
【解析】
(Ⅰ)要证明数列{nan}是等比数列,应先求其通项公式,然后用等比数列定义证明即可。由等比数列通向公式可求得数列{nan}的通项公式,进而可求数列{an}的通项an;(Ⅱ)要求数列{n2an}的前n项和Tn,应根据(Ⅰ)的结果求其通项公式![]() ,由通项公式的特点可用错位相减法求数列从第二项到第n项的和,再加第一项可得结果;(Ⅲ) 根据(Ⅰ)的结果,不等式
,由通项公式的特点可用错位相减法求数列从第二项到第n项的和,再加第一项可得结果;(Ⅲ) 根据(Ⅰ)的结果,不等式![]() 可变为
可变为![]() ,利用基本不等式,可求得不等式右边的最大值为
,利用基本不等式,可求得不等式右边的最大值为![]() 。可求实数λ的最小值为
。可求实数λ的最小值为![]() 。
。
(Ⅰ)[证明]:由a1+2a2+3a3+…+nan=![]() ,得a1+2a2+3a3+…+(n﹣1)an﹣1=
,得a1+2a2+3a3+…+(n﹣1)an﹣1=![]() (n≥2),
(n≥2),
①﹣②:![]() ,即
,即![]() (n≥2),∴当n≥2时,数列{nan}是等比数列,
(n≥2),∴当n≥2时,数列{nan}是等比数列,
又a1=1,a1+2a2+3a3+…+nan=![]() ,得a2=1,则2a2=2,∴
,得a2=1,则2a2=2,∴![]() ,
,
∴![]() (n≥2),∴
(n≥2),∴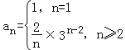 ;
;
(Ⅱ)解:由(Ⅰ)可知![]() ,
,
∴Tn=1+2×2×30+2×3×31+2×4×32+…+2n×3n﹣2,则![]() ,
,
两式作差得:![]() ,得:
,得:![]() ;
;
(Ⅲ)解:由![]() ≤(n+6)λ,得
≤(n+6)λ,得![]() ≤(n+6)λ,
≤(n+6)λ,
即![]() 对任意n∈N*恒成立.
对任意n∈N*恒成立.
当n=2或n=3时n+![]() 有最小值为5,
有最小值为5,![]() 有最大值为
有最大值为![]() ,故有λ≥
,故有λ≥![]() ,∴实数λ的最小值为
,∴实数λ的最小值为![]() .
.

练习册系列答案
相关题目