题目内容
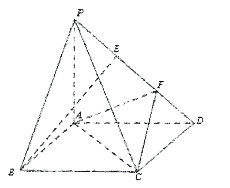
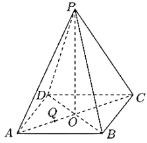
【题目】以下是我们常见的空间几何体.
（1） （2） （3） （4） （5） （6） （7） （8） （9）（10）
（11）
（1）以上几何体中哪些是棱柱？
（2）一个几何体为棱柱的充要条件是什么？
（3）如何求以上几何体的表面积？
【答案】（1）（2）（4）（6）（7）.
（2）两个面互相平行，且多面体的顶点都在这两个面上，其余各面都是平行四边形.
（3）各个面的面积之和.
【解析】
（1）根据棱柱的定义进行筛选，即可得出结论；
（2）根据棱柱侧棱平行且相等，顶点都在平行平面上，即可得出结论；
（3）根据表面积的定义，即可求解.
（1）根据棱柱的定义：有两个面互相平行，其余各面都是四边形，
并且每相邻两个四边形的公共边都互相平行，由这些面所围成的
多面体为棱柱.可知（1）（2）（4）（6）（7）为棱柱；
（2）一个几何体为棱柱的充要条件是：两个面互相平行，
且多面体的顶点都在这两个面上，其余各面都是平行四边形.
（3）求解几何体的表面积即求各个面的面积之和.
练习册系列答案
相关题目
【题目】每年春节，各地的餐馆都出现了用餐需预定的现象，致使一些人在没有预定的情况下难以找到用餐的餐馆，针对这种现象，专家对人们的用餐地点及性别作出调查，得到的情况如下表所示：
在家用餐 | 在餐馆用餐 | 总计 | |
男性 | 30 | ||
女性 | 40 | ||
总计 | 50 | 100 |
（1）完成上述
列联表；
（2）根据表中的数据，试通过计算判断是否有
的把握说明用餐地点与性别有关？
参考公式及数据：
，其中
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |