题目内容
13.已知正数a,b满足a+b+ab=1,求a+b的取值范围.分析 由题意和基本不等式可得1-(a+b)=ab≤$(\frac{a+b}{2})^{2}$,解关于a+b的不等式再结合已知式子可得.
解答 解:∵正数a,b满足a+b+ab=1,
∴1-(a+b)=ab≤$(\frac{a+b}{2})^{2}$,
整理可得(a+b)2+4(a+b)-4≥0,
解不等式可得a+b≥2$\sqrt{2}$-2,或a+b≤-2-2$\sqrt{2}$(舍去),
又a+b=1-ab<1,
∴a+b的取值范围为[2$\sqrt{2}$-2,1)
点评 本题考查基本不等式,涉及不等式的解法和整体法,属基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目




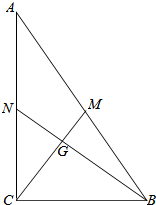 如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.
如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.