题目内容
1.已知4(x2+y2)=2xy+z(x,y≠0,z>0),且当|2x+y|取最大值时,($\frac{3}{x}$-$\frac{4}{y}$+$\frac{5}{z}$)的最小值为-5.分析 当|2x+y|取最大值时得到x=2y,代入4(x2+y2)=2xy+z求出z=16y2,将($\frac{3}{x}$-$\frac{4}{y}$+$\frac{5}{z}$)中的x,z换成y,得到关于y的二次函数,通过配方求出其最小值即可.
解答 解:若|2x+y|取最大值,即(2x+y)2取得最大值,
而(2x+y)2=4x2+4xy+y2=6xy-3y2+z=3y(2x-y)+z,
≤(3y)2+(2x-y)2+z,(z>0),
∴当且仅当3y=2x-y时取“=”,此时:x=2y,
∴由4(x2+y2)=2xy+z得:z=16y2,
∴$\frac{3}{x}$-$\frac{4}{y}$+$\frac{5}{z}$=$\frac{3}{2y}$-$\frac{4}{y}$+$\frac{5}{1{6y}^{2}}$=5${(\frac{1}{4y}-1)}^{2}$-5≥-5,
故答案为:-5.
点评 本题考查基本不等式,由|2x+y|取最大值得到x=2y是关键,考查配方法求最值,属于中档题.

练习册系列答案
相关题目
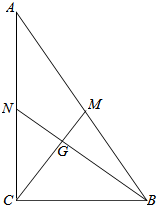 如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.
如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.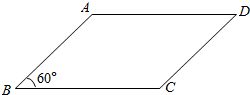 如图所示,已知菱形ABCD,∠B=60°,现以AB为轴,菱形ABCD绕AB旋转一周,画出几何体的大致形状,并指明它是由哪些简单几何体组成?
如图所示,已知菱形ABCD,∠B=60°,现以AB为轴,菱形ABCD绕AB旋转一周,画出几何体的大致形状,并指明它是由哪些简单几何体组成?