题目内容
已知n∈N*,设Sn是单调递减的等比数列{an}的前n项和,a1=1,且S2+a2、S4+a4、S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列x∈(0,+∞)满足b1=2a1,bn+1bn+bn+1-bn=0,求数列f(x)max≤0的通项公式;
(Ⅲ)在满足(Ⅱ)的条件下,若cn=
,求数列{cn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列x∈(0,+∞)满足b1=2a1,bn+1bn+bn+1-bn=0,求数列f(x)max≤0的通项公式;
(Ⅲ)在满足(Ⅱ)的条件下,若cn=
| ancos(nπ) |
| bn |
( I)设数列{an}的公比为q,由2(S4+a4)=S2+a2+S3+a3,
得(S4-S2)+(S4-S3)+2a4=a2+a3,即4a4=a2,
所以q2=
,
∵{an}是单调数列,
∴q=
,
∴an=(
)n-1.
( II)b1=2,∵bn+1bn+bn+1-bn=0,
∴1+
-
=0,即
-
=1,
即{
}是以
为首项,1为公差的等差数列,
故
=
+(n-1)×1=
,即bn=
.
( III)∵cn=
=
cos(nπ)=
•(-1)n=(2n-1)×(-
)n,
∴Tn=1×(-
)+3×(-
)2+5×(-
)3+…+(2n-1)×(-
)n,
-
Tn=1×(-
)2+3×(-
)3+…+(2n-3)×(-
)n+(2n-1)×(-
)n+1,
两式相减,得
Tn=1×(-
)+2[(-
)2+(-
)3+…+(-
)n-(2n-1)×(-
)n+1]
=
+2×
-(2n-1)×(-
)n+1
=
-
[1-(-
)n]-(2n-1)×(-
)n+1,
=-
+(n+
)•(-
)n,
即Tn=-
+
(6n+1)(-
)n.
得(S4-S2)+(S4-S3)+2a4=a2+a3,即4a4=a2,
所以q2=
| 1 |
| 4 |
∵{an}是单调数列,
∴q=
| 1 |
| 2 |
∴an=(
| 1 |
| 2 |
( II)b1=2,∵bn+1bn+bn+1-bn=0,
∴1+
| 1 |
| bn |
| 1 |
| bn+1 |
| 1 |
| bn+1 |
| 1 |
| bn |
即{
| 1 |
| bn |
| 1 |
| 2 |
故
| 1 |
| bn |
| 1 |
| 2 |
| 2n-1 |
| 2 |
| 2 |
| 2n-1 |
( III)∵cn=
| ancos(nπ) |
| bn |
| 2n-1 |
| 2n |
| 2n-1 |
| 2n |
| 1 |
| 2 |
∴Tn=1×(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
两式相减,得
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
-
| ||||
1+
|
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
即Tn=-
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 2 |

练习册系列答案
相关题目
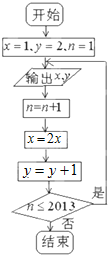
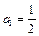 ,则
,则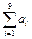 = .
= .