题目内容
6.已知抛物线y2=8x的焦点为F,过点F作直线交抛物线于点A,B,点M为AB的中点,过点M作准线的垂线,交抛物线于点P,若|FP|=$\frac{5}{2}$,则|AB|=( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
分析 求出抛物线焦点为F(2,0),准线为l:x=-2.设A(x1,y1)、B(x2,y2),直线AB的方程为y=k(x-2),由AB方程与抛物线方程消去y得关于x的一元二次方程,利用根与系数的关系算出:x1+x2=4+$\frac{8}{{k}^{2}}$,x1x2=4,由此算出P的坐标为P($\frac{2}{{k}^{2}}$,$\frac{4}{k}$),根据|FP|=$\frac{5}{2}$,利用点到两点间的距离公式解出k2=4,从而算出x1+x2=6,最后根据抛物线的定义,可得弦长|AB|的值.
解答 解:∵抛物线方程为y2=8x,
∴2p=8,p=4,可得抛物线的焦点为F(2,0),准线为l:x=-2,
设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-2),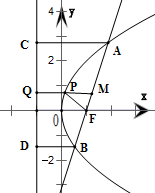
由$\left\{\begin{array}{l}{y=k(x-2)}\\{{y}^{2}=8x}\end{array}\right.$消去y,得k2x2-(4k2+8)x+4k2=0,
∴x1+x2=4+$\frac{8}{{k}^{2}}$,x1x2=4,
∵过AB的中点M作准线的垂线与抛物线交于点P,
∴设P的坐标为(x0,y0),可得y0=$\frac{1}{2}$(y1+y2),
∵y1=k(x1-2),y2=k(x2-2),
∴y1+y2=k(x1+x2)-4k=k•(4+$\frac{8}{{k}^{2}}$)-4k=$\frac{8}{k}$,
得到y0=$\frac{1}{2}$$•\frac{8}{k}$=$\frac{4}{k}$,所以x0=$\frac{1}{8}$y02=$\frac{2}{{k}^{2}}$,可得P($\frac{2}{{k}^{2}}$,$\frac{4}{k}$).
∵|FP|=$\frac{5}{2}$,∴$\sqrt{(2-\frac{2}{{k}^{2}})^{2}+\frac{16}{{k}^{2}}}$=$\frac{5}{2}$,解之得k2=4,
因此x1+x2=4+$\frac{8}{4}$=6,
根据抛物线的定义可得|AB|=x1+x2+p=6+4=10.
故选B.
点评 本题给出抛物线满足的条件,求抛物线经过焦点的弦AB的长.着重考查了抛物线的定义、标准方程与简单几何性质的知识,考查了直线与圆锥曲线的位置关系,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
| A. | (2,0) | B. | (0,2) | C. | (1,0) | D. | (0,1) |
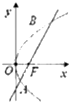 已知抛物线y2=2px(p>0)的准线方程为x=-1,斜率为1的直线过抛物线的焦点F,且与抛物线交于A、B两点,求线段AB的长度.
已知抛物线y2=2px(p>0)的准线方程为x=-1,斜率为1的直线过抛物线的焦点F,且与抛物线交于A、B两点,求线段AB的长度. 根据最新修订的《环境空气质量标准》指出空气质量指数在0:50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.
根据最新修订的《环境空气质量标准》指出空气质量指数在0:50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.