题目内容
1.抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过A的直线l交C于另一点B,交x轴的正半轴于点D,有|FA|=|FD|,又直线l1∥l,且l1与C有唯一公共点E.(1)证明:直线AE过x轴上一定点,并求出定点的坐标;
(2)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
分析 (1)由抛物线C:y2=2px(p>0)可得焦点F$(\frac{p}{2},0)$,设A(x0,y0)(x0,y0≠0),D(xD,0)(xD>0),由于|FA|=|FD|,可得$|{x}_{D}-\frac{p}{2}|={x}_{0}+\frac{p}{2}$,由xD>0,可得D(x0+p,0).直线AB的斜率为kAB=$-\frac{{y}_{0}}{p}$.由于直线l1∥l,可设直线l1的方程为:$y=-\frac{{y}_{0}}{p}x+m$,与抛物线方程联立可化为$\frac{{y}_{0}}{2{p}^{2}}{y}^{2}+y-m=0$,由△=0,可得m=-$\frac{{p}^{2}}{2{y}_{0}}$.得到yE=$-\frac{{p}^{2}}{{y}_{0}}$,xE=$\frac{{p}^{3}}{2{y}_{0}^{2}}$,利用斜率计算公式可得kAE=kAF,即可得出.
(II)由(I)可知:直线AE过焦点F$(\frac{p}{2},0)$.可得|AE|=|AF|+|FE|=${x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p$,设直线AE的方程为x=ty+$\frac{p}{2}$,可得t=$\frac{{x}_{0}-\frac{p}{2}}{{y}_{0}}$,设B(x1,y1),直线AB的方程为:$y-{y}_{0}=-\frac{{y}_{0}}{p}(x-{x}_{0})$,代入抛物线方程可得:${y}_{1}=-{y}_{0}-\frac{2{p}^{2}}{{y}_{0}}$,x1=${x}_{0}+2p+\frac{{p}^{2}}{{x}_{0}}$,再利用点到直线的距离公式可得S△ABE=$\frac{1}{2}|AB|•d$=$\sqrt{2p}$$({x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p)^{\frac{3}{2}}$,利用基本不等式的性质即可得出.
解答 (1)证明:由抛物线C:y2=2px(p>0)可得焦点F$(\frac{p}{2},0)$,
设A(x0,y0)(x0,y0≠0),D(xD,0)(xD>0),
∵|FA|=|FD|,
∴$|{x}_{D}-\frac{p}{2}|={x}_{0}+\frac{p}{2}$,由xD>0,可得xD=x0+p,因此D(x0+p,0),
∴直线AB的斜率为kAB=$-\frac{{y}_{0}}{p}$.
∵直线l1∥l,
∴可设直线l1的方程为:$y=-\frac{{y}_{0}}{p}x+m$,
联立$\left\{\begin{array}{l}{y=-\frac{{y}_{0}}{p}x+m}\\{{y}^{2}=2px}\end{array}\right.$,化为$\frac{{y}_{0}}{2{p}^{2}}{y}^{2}+y-m=0$,
由△=0,可得m=-$\frac{{p}^{2}}{2{y}_{0}}$.
则yE=$-\frac{{p}^{2}}{{y}_{0}}$,xE=$\frac{{p}^{3}}{2{y}_{0}^{2}}$,
当${y}_{0}^{2}≠{p}^{2}$时,kAE=$\frac{{y}_{E}-{y}_{0}}{{x}_{E}-{x}_{0}}$=$\frac{2p{y}_{0}}{{y}_{0}^{2}-{p}^{2}}$=$\frac{{y}_{0}}{{x}_{0}-\frac{p}{2}}$=kAF,
因此直线AE过焦点F$(\frac{p}{2},0)$.
(II)由(I)可知:直线AE过焦点F$(\frac{p}{2},0)$.
∴|AE|=|AF|+|FE|=${x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p$,
设直线AE的方程为x=ty+$\frac{p}{2}$,∵点A在直线AE上,
∴t=$\frac{{x}_{0}-\frac{p}{2}}{{y}_{0}}$,
设B(x1,y1),直线AB的方程为:$y-{y}_{0}=-\frac{{y}_{0}}{p}(x-{x}_{0})$,
由y0≠0,可得x=$-\frac{p}{{y}_{0}}y+p+{x}_{0}$,代入抛物线方程可得:${y}_{1}=-{y}_{0}-\frac{2{p}^{2}}{{y}_{0}}$,x1=${x}_{0}+2p+\frac{{p}^{2}}{{x}_{0}}$,
故点B到直线AE的距离d=$\frac{|\frac{{p}^{2}}{{x}_{0}}+{x}_{0}+2p+t({y}_{0}+\frac{2{p}^{2}}{{y}_{0}})-\frac{p}{2}|}{\sqrt{1+{t}^{2}}}$=$2\sqrt{2p}$$\sqrt{{x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p}$,
则S△ABE=$\frac{1}{2}|AB|•d$=$\frac{1}{2}({x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p)$$•2\sqrt{2p}$$\sqrt{{x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p}$=$\sqrt{2p}$$({x}_{0}+\frac{{p}^{2}}{4{x}_{0}}+p)^{\frac{3}{2}}$≥4p2,当且仅当${x}_{0}=\frac{p}{2}$时取等号,
因此△ABE的面积存在最小值为4p2.
点评 本题考查了抛物线的定义标准方程及其性质、直线与抛物线相交转化为方程联立可得根与系数的关系及交点坐标、弦长公式、点到直线的距离公式、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


| A. | $4\sqrt{2}$ | B. | $2\sqrt{10}$ | C. | $2\sqrt{13}$ | D. | $2\sqrt{15}$ |
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{8}{3}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 2 |
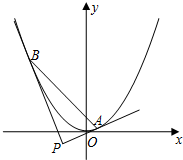 已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.
已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.