题目内容
17.已知A,B是抛物线C:y2=2px(p>0)上不同的两点,点D在抛物线C的准线l上,且焦点F到直线x-y+2=0的距离为$\frac{3\sqrt{2}}{2}$.(1)求抛物线C的方程;
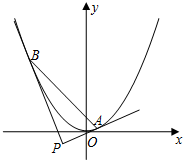
(2)若直线AB过焦点F,且直线AD过原点O,求证:直线BD平行x轴.
分析 (1)求出抛物线的焦点,由点到直线的距离公式,解得p=2,进而得到抛物线方程;
(2)求得抛物线的焦点和准线方程,设直线AB:x=ty+1,A(x1,y1),B(x2,y2),联立抛物线方程,运用韦达定理,再设直线AD:y=$\frac{{y}_{1}}{{x}_{1}}$x,求得D的坐标,通过B,D的纵坐标,即可得证.
解答 (1)解:抛物线C:y2=2px的焦点F($\frac{p}{2}$,0),
由题意可得d=$\frac{|\frac{p}{2}-0+2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
解得p=2,
即有抛物线方程为y2=4x;
(2)证明:抛物线y2=4x的焦点F(1,0),
准线方程为x=-1,
设直线AB:x=ty+1,A(x1,y1),B(x2,y2),
联立抛物线方程,可得y2-4ty-4=0,
即有y1y2=-4,
直线AD:y=$\frac{{y}_{1}}{{x}_{1}}$x,
则有D(-1,-$\frac{{y}_{1}}{{x}_{1}}$),
由于-$\frac{{y}_{1}}{{x}_{1}}$=-$\frac{4{y}_{1}}{{{y}_{1}}^{2}}$=-$\frac{4}{{y}_{1}}$=y2,
故直线BD平行x轴.
点评 本题考查抛物线的方程和性质,主要考查直线方程和抛物线方程联立,运用韦达定理,同时考查点到直线的距离公式的运用,属于中档题.

练习册系列答案
相关题目
5.某学校餐厅每天供应500名学生用餐,每星期一有A,B两种菜可供选择.调查资料表明,凡是在星期一选A种菜的学生,下星期一会有20%改选B种菜;而选B种菜的学生,下星期一会有30%改选A种菜.用an,bn分别表示在第n个星期的星期一选A种菜和选B种菜的学生人数,若a1=300,则an+1与an的关系可以表示为( )
| A. | an+1=$\frac{1}{2}{a_n}$+150 | B. | an+1=$\frac{1}{3}{a_n}$+200 | C. | an+1=$\frac{1}{5}{a_n}$+300 | D. | an+1=$\frac{2}{5}{a_n}$+180 |
6.定义域为D的单调函数y=f(x),如果存在区间[m,n]⊆D,满足当定义域为是[m,n]时,f(x)的值域也是[m,n],则称[m,n]是该函数的“可协调区间”;如果函数y=$\frac{({a}^{2}+a)x-1}{{a}^{2}x}$(a≠0)的一个可协调区间是[m,n],则实数a的取值范围是( )
| A. | -3<a<1 | B. | -3<a<0 | C. | 0<a<1 | D. | a<-3或a>1 |
5.抛物线x2=y的准线方程是( )
| A. | x=$\frac{1}{2}$ | B. | y=$\frac{1}{2}$ | C. | x=-$\frac{1}{4}$ | D. | $y=-\frac{1}{4}$ |
 已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.
已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.