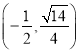题目内容
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求函数![]() 及
及![]() 的解析式,并用函数单调性的定义证明:函数
的解析式,并用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,证明见解析;(2)
,证明见解析;(2)![]()
【解析】
(1)根据![]() ,用
,用![]() 代替式子中的
代替式子中的![]() ,利用奇偶性,构造方程组,解出
,利用奇偶性,构造方程组,解出![]() 和
和![]() 的解析式,取任意的
的解析式,取任意的![]() ,且
,且![]() ,对
,对![]() 进行化简,判断出
进行化简,判断出![]() ,从而证明;(2)先得到
,从而证明;(2)先得到![]() 的解析式,令
的解析式,令![]() ,判断出
,判断出![]() 的值域,从而得到
的值域,从而得到![]() 的值域,根据方程有解,从而得到
的值域,根据方程有解,从而得到![]() 的取值范围.
的取值范围.
(1)因为![]() 为奇函数,
为奇函数,![]() 为偶函数,
为偶函数,
所以![]() .
.
又因为![]() ①
①
所以![]() 代替式子中的
代替式子中的![]() ,得到
,得到
![]() ,即
,即![]() ②
②
联立①②,可得
![]()
![]() ,
,![]()
设任意的![]() ,且
,且![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]()
![]()
所以![]() ,即
,即![]() ,所以
,所以![]() 0
0
所以![]() ,即函数
,即函数![]() 在
在![]() 上是减函数
上是减函数
(2)因为![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,为单调递减函数,
,为单调递减函数,
因为![]() 的定义域为
的定义域为![]() ,
,
所以![]() ,得到
,得到![]()
即![]() 的定义域为
的定义域为![]()
即![]() ,
,
所以![]() , 则
, 则![]() ,
,
因为关于![]() 的方程
的方程![]() 有解,
有解,
故![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】某桶装水经营部每天的房租、人员工资等固定成本为300元,每桶水的进价是8元,销售单价与日均销售量的关系如表所示:
销售单价/元 | 9 | 10 | 11 | 12 | 13 | 14 |
日均销售量/桶 | 550 | 500 | 450 | 400 | 350 | 300 |
请根据以上数据分析,这个店怎样定每桶水的单价才能获得最大利润?最大利润是多少?